Part 1

You are given a positive integer $N. Write a script to find out all possible combination of Fibonacci Numbers required to get $N on addition.

Solution

Sample Run

$ perl perl/ch-1.pl 6
1 + 5 = 6
1 + 2 + 3 = 6
1 + 5 = 6
1 + 2 + 3 = 6

$ perl perl/ch-1.pl 9
1 + 8 = 9
1 + 3 + 5 = 9
1 + 8 = 9
1 + 3 + 5 = 9
1 + 1 + 2 + 5 = 9

Notes

The approach here is to generate all Fibonacci terms up to $n and then evaluate all combinations of these terms and see which sum to $n. The most interesting part here is perhaps how the combinations are generated. Here we are making use of a convenient property that there are 2^n -1 subsets of the set {1..n}. So we generate numbers $b as an n-digit binary number using sprintf. We correspond the binary digits of k to indices into the Fibonacci sequence and select a Fibonacci term if its bit value is 1.

Also note that the Fibonacci sequence starts off as 1, 1, 2, 3, 5, … and so while we may see two 1s these are separate, and not repeated, Fibonacci terms.

Part 2

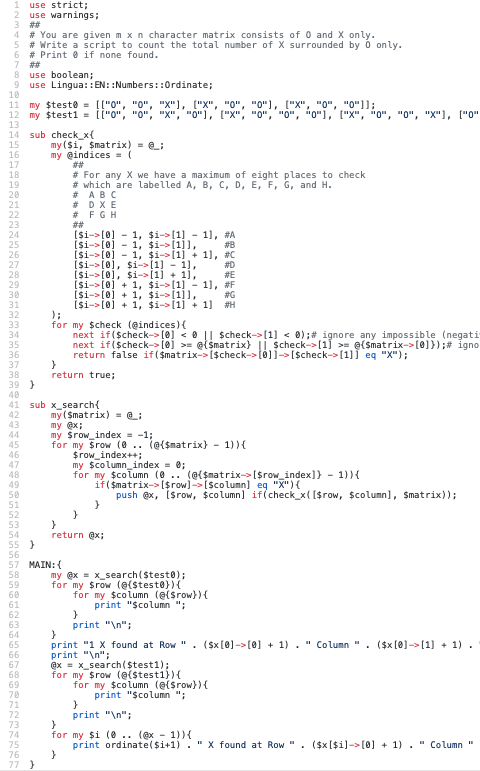
You are given m x n character matrix consists of O and X only. Write a script to count the total number of X surrounded by O only. Print 0 if none found.

Sample Run

perl perl/ch-2.pl
O O X
X O O
X O O
1 X found at Row 1 Column 3.

O O X O
X O O O
X O O X
O X O O
1st X found at Row 1 Column 3.
2nd X found at Row 3 Column 4.

Notes

I made use of Neil Bowers Lingua::EN::Numbers::Ordinate to make the output look a little nicer.

Otherwise think this is straight forward enough…for each test matrix identify the Xs and then check to see if they are “lonely”. The number of possible adjacent space to check is no more than eight as shown in the code so we check these all, if they exist.