RabbitFarm

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 5.

Part 1: Good Integer

You are given a positive integer, $int, having 3 or more digits. Write a script to return the Good Integer in the given integer or -1 if none found.

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re just specifying to use the current version of Perl, for all the latest features in the language. This fragment is also used in Part 2.

A good integer is exactly three consecutive matching digits.

Now all we need are a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
444 
-1 
000
    

Part 2: Changing Keys

You are given an alphabetic string, $str, as typed by user. Write a script to find the number of times user had to change the key to type the given string. Changing key is defined as using a key different from the last used key. The shift and caps lock keys won’t be counted.

Finally, here’s a few tests to confirm everything is working right.

Sample Run

$ perl ch-2.pl 
3 
0 
1
    

References

The Weekly Challenge 282
Generated Code

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 6.

Part 1: Check Color

You are given coordinates, a string that represents the coordinates of a square of the chessboard. Write a script to return true if the square is light, and false if the square is dark.

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re just specifying to use the current version of Perl, for all the latest features in the language. This fragment is also used in Part 2.

The color of a given square is determined by calculating its color number. If the color number is positive the square is dark. If the color number is negative then it is light.

We determine the color number in the following code fragment. Here we compute $n as -1 raised tot he power of the letter’s index. In this way we get alternating -1/1 starting with ’a’. We do the same with the second part of the co-rdinate to get an alternating -1/1 for the chessboard row. These are multiplied together to get the color number.

Now all we need are a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
true 
false 
true 
true 
false 
true 
false
    

Part 2: Knight’s Move

A Knight in chess can move from its current position to any square two rows or columns plus one column or row away. Write a script which takes a starting position and an ending position and calculates the least number of moves required.

The bulk of the code is just setting up the main data structure, a graph. For each square of the chessboard we add an edge to all the squares that are reachable by a knight.

For convenience I use a little bit of nuweb hackery instead of a new subroutine to seperate out this code which is repeated in the final generated code file.

After we go through the work of setting up the graph the result can be easily gotten via use of Djikstra’s shortest path algorithm.

Finally, here’s a few tests to confirm everything is working right.

Sample Run

$ perl ch-2.pl 
g2 ---> a8
4: g2 -> e3 -> c4 -> b6 -> a8
g2 ---> h2
3: g2 -> e1 -> f3 -> h2
 

References

The Weekly Challenge 281
Generated Code
Graph.pm
Knight’s Tours

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 5.

Part 1: Twice Appearance

You are given a string, $str, containing lowercase English letters only. Write a script to print the first letter that appears twice.

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re just specifying to use the current version of Perl, for all the latest features in the language. This fragment is also used in Part 2.

Now all we need are a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
d 
c 
a
    

Part 2: Count Asterisks

You are given a string, $str, where every two consecutive vertical bars are grouped into a pair. Write a script to return the number of asterisks, *, excluding any between each pair of vertical bars.

This is our principal function. As can be seen, it’s very short! The logic here is simple: peel off pairs and use a regex to find the asterisks.

Finally, here’s a few tests to confirm everything is working right.

Sample Run

$ perl ch-2.pl 
13 
30 
37
    

References

The Weekly Challenge 280
Generated Code

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 5.

Part 1: Defang IP Address

You are given a valid IPv4 address. Write a script to return the defanged version of the given IP address. A defanged IP address replaces every period “.” with “[.]".

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re just specifying to use the current version of Perl, for all the latest features in the language. This fragment is also used in Part 2.

First, let’s consider how we know to make string substitutions. Regular Expressions are an obvious choice. Maybe a little too obvious to be fun. We could also convert the string to a list of characters and then loop over the list making adjustments as necessary. That sounds nicer. Instead of some ordinary loop though let’s add a little recursive spice!

Now all we need are a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
1[.]1[.]1[.]1 
255[.]101[.]1[.]0
    

Part 2: String Score

You are given a string, $str. Write a script to return the score of the given string. The score of a string is defined as the sum of the absolute difference between the ASCII values of adjacent characters.

We’ll contain the solution in a single function. The completed solution will just have that function plus a few tests. Instead of recursion this time we’ll use a redo block.

This is our principal function. As can be seen, it’s very short! The logic here is simple: peel off characters until there’s just one left. Calculate the string score each time through. Well, to simplify things we’ll first actually convert the characters to their ascii values. That’s what the map at the start of the function does.

Finally, here’s a few tests to confirm everything is working right.

Sample Run

$ perl ch-2.pl 
13 
30 
37
    

References

The Weekly Challenge 272
Generated Code

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 7.

Part 1: Element Digit Sum

You are given an array of integers, @integers. Write a script to evaluate the absolute difference between every element and the digit sum of the entire given array.

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re just specifying to use the current version of Perl, for all the latest features in the language. This fragment is also used in Part 2.

First, let’s consider how we compute the digit sum for an array of integers. If we we make sure that all multi-digit numbers are expanded into lists of digits then this is the sum of the concatenation of all such lists, along with single digit numbers.

The expansion of multi-digit numbers is handled by map, and the sum is taken with unpack and the resulting final array. A key thing to remember here is that Perl will flatten all lists inside the array so all the results from the map will be in a list of single digits.

The element sum is the same procedure as the digit sum, but just without the map.

Finally, we have a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
36 
9 
0 
1296
    

Part 2: Multiply by Two

You are given an array of integers, @integers and an integer $start. Write a script to do the following:

a) Look for $start in the array @integers, if found multiply the number by 2.

b) If not found stop the process, otherwise repeat.

In the end return the final value.

We’ll contain the solution in a single recursive function. The completed solution will just have that function plus a few tests.

This is our principal function. As can be seen, it’s very short! The logic here is simple: for each recursive call check for $start in the array and, if found, double $start and keep recursing. Otherwise, return $start.

Finally, here’s a few tests to confirm everything is working right.

Sample Run

$ perl ch-2.pl 
24 
8 
2
    

References

The Weekly Challenge 261
Generated Code

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

File Index

"ch-1.pl" Defined by 1.

"ch-2.pl" Defined by 5.

Part 1: Unique Occurrences

You are given an array of integers, @ints. Write a script to return 1 if the number of occurrences of each value in the given array is unique or 0 otherwise.

The complete solution is contained in one file that has a simple structure.

For this problem we do not need to include very much. We’re specifying to use the current version of Perl, for all the latest features. We’re also using the boolean module, for the convenience of returning and displaying the return values.

This fragment is also used in Part 2.

Here we have a single function which does essentially all the work. First we loop through the array of numbers and count occurrences. Then the counts are themselves used as hash keys to eliminate duplicates. If no duplicates are removed then the number of these new keys is equal to the number of original count values.

Finally, we have a few lines of code for running some tests.

Sample Run

$ perl perl/ch-1.pl 
1 
0 
1
    

Part 2: Dictionary Rank

You are given a word, $word. Write a script to compute the dictionary rank of the given word.

The solution to the second part of this week’s challenge is a little more complex than the first part. In the solution file we define our own function for computing all permutations of an array, which is then used to determine the dictionary rank.

This function is a recursive implementation of Heap’s algorithm. A lot has been written on this algorithm, so I won’t go into much detail here.

Now that we have a way to compute all permutations we will use that to determine the dictionary rank. There is a trick here. Keep in mind that dictionaries do not have multiple entries for repeated words! In the case of words with repeated letters than there will be permutations that are effectively equal in that they contain the same letters. Although they are created by permuting equal (but different) letters for ranking purposes we will consider them the same.

Sample Run

$ perl ch-2.pl 
3 
88 
255
    

References

The Weekly Challenge 260
Generated Code
Heap’s Algorithm

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1: Banking Day Offset

You are given a start date and offset counter. Optionally you also get bank holiday date list. Given a number (of days) and a start date, return the number (of days) adjusted to take into account non-banking days. In other words: convert a banking day offset to a calendar day offset.

Non-banking days are:

(a)

Weekends

(b)

Bank holidays

Using Time::Piece the work can be contained in a single function. Really the main piece of logic required of sub count_days() is for us to check if a day is a weekend or bank holiday.

The rest of the code just tests this function.

Sample Run

$ perl perl/ch-1.pl 
2018-07-04 
2018-07-03
    

Part 2: Line Parser

You are given a line like below:

{% id field1=“value1”field2=“value2”field3=42 %}

Where

(a)

“id”can be \w+.

(b)

There can be 0 or more field-value pairs.

(c)

The name of the fields are \w+.

(d)

The values are either number in which case we don’t need double quotes or string in which case we need double quotes around them.

The line parser should return a structure like:

{ 
       name => id, 
       fields => { 
           field1 => value1, 
           field2 => value2, 
           field3 => value3, 
       } 
}
    

It should be able to parse the following edge cases too:

{%  youtube title="Title␣\"quoted\"␣done" %}
    

and

{%  youtube title="Title␣with␣escaped␣backslash␣\\" %}
    

Most of the work is done in a parser constructed using Parse::Yapp.

ch-2.pl

First off, before we get into the parser, here is a small bit of code for driving the tests.

The rest of the code drives some tests.

The Parser

Here is where the work is really done. Parse::Yapp is given the following grammar. A parser is generated, contained in it’s own module.

First off is the grammar’s header. Here we define the symbols used in the rules which follow. We also add a small code block which contains a hash for holding the structure obtained from the parsed text.

Here is the most important section, the rules for processing the input! For some rules we have also added action code blocks. We want to construct a data structure from the given input and in these action code blocks that final result is accumulated. Remember, the first rule is going to be called last, when the input is complete, so there we give a reference to a hash containing the result. This is the return value for the parse function found in the grammar’s footer.

The footer contains additional Perl code for the lexer, error handing, and a parse function which provides the main point of execution from code that wants to call the parser that has been generated from the grammar.

The lexer function is called repeatedly for the entire input. Regular expressions are used to identify symbols (the ones declared in the header) and pass them along for the rules processing.

The parse function is for the convenience of calling the generated parser from other code. yapp will generate a module and this will be the module’s method used by other code to execute the parser against a given input.

Notice here that we are squashing white space, both tabs and spaces, using tr. This reduces all repeated tabs and spaces to a single one. The eases further processing since extra whitespace is just ignored, according to the rules we’ve been given.

Also notice the return value from parsing. In the rules section we provide a return value, a hash reference, in the final action code block executed.

This is really just about the most minimal error handling function there can be! All this does is print “syntax error”when the parser encounters a problem.

Sample Run

$ yapp -m Ch2 perl/ch-2.yp; mv Ch2.pm perl; perl -I. ch-2.pl 
{%  id    field1="value1"    field2="value2"    field3=42 %} 
{ 
        name => id 
        fields => { 
                field1 =>  value1 
                field2 =>  value2 
                field3 =>  42 
        } 
} 
{%  youtube title="Title␣\"quoted\"␣done" %} 
{ 
        name => youtube 
        fields => { 
                field1 =>  value1 
                field2 =>  value2 
                field3 =>  42 
                title =>  Title 
        } 
} 
{%  youtube title="Title␣with␣escaped␣backslash␣\\" %} 
{ 
        name => youtube 
        fields => { 
                field1 =>  value1 
                field2 =>  value2 
                field3 =>  42 
                title =>  Title 
        } 
}
    

File Index

"perl/ch-1.pl" Defined by 4.

"perl/ch-2.pl" Defined by 8.

"perl/ch-2.yp" Defined by 17.

References

The Weekly Challenge 259
Generated Code

The standard way that graphs are taught in Prolog is to represent the graph edges in the Prolog database and then, as needed, manipulate the database using assertz/1 and retract/1. There really is nothing wrong with this for many applications. However, when dealing with large graphs the overhead of writing to the database may not be worth the performance gain (via indexing) when querying. Especially in cases when the amount of querying may be low, there may not be any “return on investment”.

An alternative method, promoted by Markus Triska, is the use of attributed variables. In this way a variable represents a graph node and the attributes represent edges. Additionally, beyond that basic representation, additional attributes can be used for other information on the node and to add attributes to the edges such as a weight or other information on the relationship between nodes.

To be clear, attributed variables are primarily intended for use when building libraries, such as for constraint logic programming. There the default Prolog unification algorithm is less convenient than an extended version using attributed variables. In these cases hooks are used to determine, say, domain constraints on variables. Here will not concern ourselves with such advanced topics!

Not all Prologs provide attributed variables. Scryer and SWI are among those that do. All of our code is implemented and tested using SWI-Prolog.

Examples

Let’s start off with the most basic example: a small set of otherwise meaningless nodes connected at random.

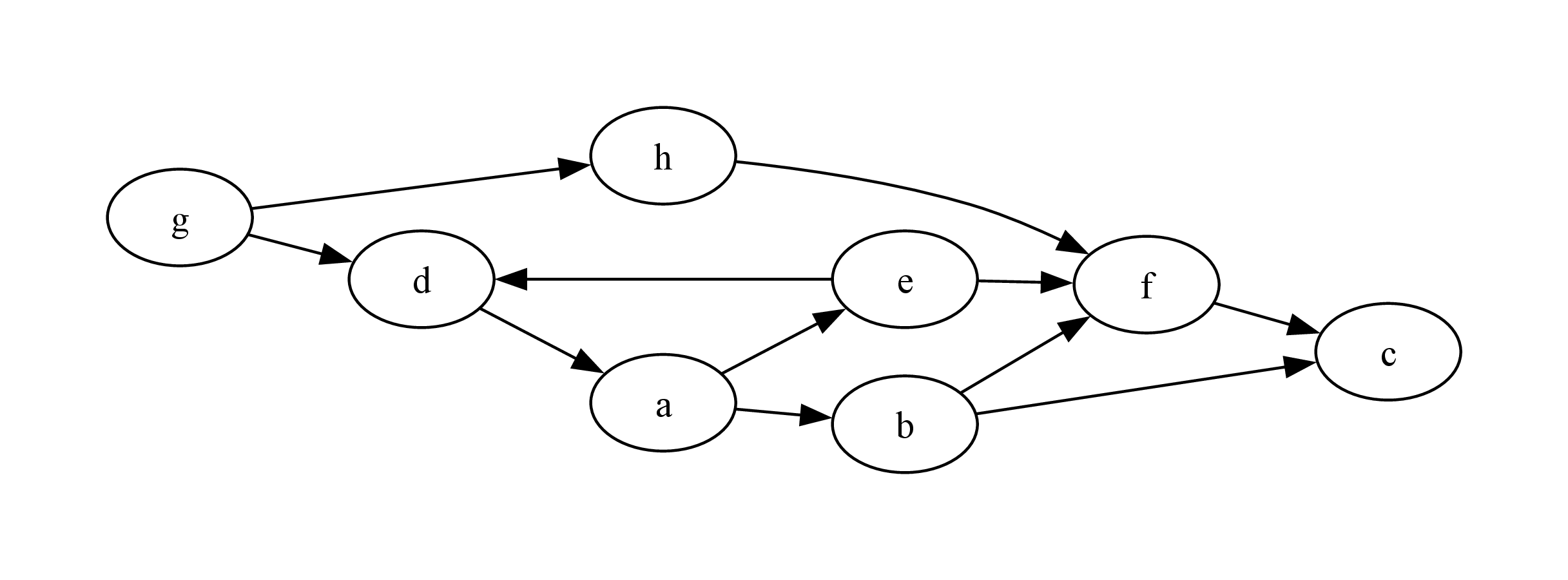
This small graph, adapted from an example in Clocksin’s Clause and Effect, can be represented in Prolog in the traditional way as follows.

As needed additional edges can be added and removed from the Prolog database dynamically using assertz/1 and retract/1.

How might we change this to an attributed variables representation?

First off, we need to keep in mind that only an uninstantiated variable can have an attribute set unless we also provide an attribute hook. Since we otherwise have no need for a hook, we will restrict ourselves to having only uninstantiated variables as nodes. Of course, we need to maintain information for each node and edge. In both cases the node information and the edge information are kept as attributes. At first this sounds more complicated than it really is. Let’s see how it comes together in practice.

To build a bridge from the old to the new we will first create a predicate, edges_attributed/2 which converts a list of edges (e.g. [edge(a, b), edge(b, f), edge(f, c)]) to a list of attributed variables where the edges are attributes on the nodes. The attributes on each node are a list of edges to other node and, also, an attribute containing the node label.

For now we are only concerning ourselves with simple graphs like the example, so nodes are just unique atoms (e.g. a, b, c, ...). We’re also assuming that all edges are directed as given.

A lot of work is happening in helper predicates via maplist/3. For the most part these are just one or two lines each.

The lengthiest of the predicates used in a maplist/3 is graph_attributed/3. This is where the final assembly of the graph of attributed variables takes place.

Testing this predicate out, with just a small set of edges, we can get a sense of this new representation. A weight attribute, with default value of 1, has been added to demonstrate the possibility of attributed edge variables, but we won’t make any further use of this here.

?- Edges = [edge(a, b), edge(b, c), edge(b, d)], 
edges_attributed(Edges, Attributed). 
Edges = [edge(a, b), edge(b, c), edge(b, d)], 
Attributed = [a-_A, b-_B, c-_C, d-_D], 
put_attr(_A, node, a), 
put_attr(_A, edges, [edge(_E, a-_A, _B)]), 
put_attr(_B, node, b), 
put_attr(_B, edges, [edge(_F, b-_B, _C), edge(_G, b-_B, _D)]), 
put_attr(_C, node, c), 
put_attr(_C, edges, []), 
put_attr(_D, node, d), 
put_attr(_D, edges, []), 
put_attr(_E, weight, 1), 
put_attr(_F, weight, 1), 
put_attr(_G, weight, 1).

That looks nice, but let’s put it to work with a basic traversal.

To start with, let’s defines a predicate to determine if any two nodes are connected by a directed edge. If one or both of the two node arguments are uninstantiated then member/2 will find one for us, otherwise this will just confirm they are in the Graph, which we will be passed to all predicates that need it. This small amount of extra bookkeeping is part of the trade-off for no longer using the dynamic database.

Also, speaking of extra bookkeeping, we’ll try and maintain a level of encapsulation around the use of attributed variables. For example, in the following predicates we only need worry about the handling of attributes when determining connectedness. When building on this code for more complex purposes that is an important part of the design to keep in mind: encapsulate the low level implementation details and provide predicates which have a convenient higher level of interface.

In the spirit of building a big example, the following code does the same connectedness check, but for undirected edges. We’re not worrying too much about such graphs, but this is one way to do it.

Finally we can use this connectedness check to define path finding predicates that look a lot like any standard Prolog example of path finding you may have seen before!

Closing

At this point you should understand how to build a graph using attribute variables in Prolog. The example code here can be further extended as needed. You’ll find that this approach can take on quite a good deal of complexity!

All the code above is structured in a single file as shown. A link to this is in the References section.

Indices

Files

"graph.p" Defined by 14.

Fragments

⟨ Construct a graph of attributed variables. 6 ⟩ Referenced in 2.

⟨ Convert list of edges to attributed variables. 2 ⟩ Referenced in 14.

⟨ Create a K-V pair for each node. 8 ⟩ Referenced in 14.

⟨ Create a unique list of nodes. 4 ⟩ Referenced in 2.

⟨ Determine if two nodes are connected by a directed edge. 11 ⟩ Referenced in 14.

⟨ Determine if two nodes are connected by an undirected edge. 12 ⟩ Referenced in 14.

⟨ Example Graph (Standard) 1 ⟩ Referenced in 14.

⟨ Extract the nodes from all edges. 3 ⟩ Referenced in 2.

⟨ Find a path between any two nodes, if such a path exists. 13 ⟩ Referenced in 14.

⟨ From the node pairs, create the graph of attributed variables. 10 ⟩ Referenced in 14.

⟨ Generate attribute edge list. 9 ⟩ Referenced in 14.

⟨ Helper predicate for extracting nodes from edges. 7 ⟩ Referenced in 14.

⟨ Make the list of K-V pairs for the nodes. 5 ⟩ Referenced in 2.

References

This method has been promoted by Markus Triska on Stack Overflow, but publicly available examples are rare. Hopefully this page will be useful to any interested persons looking for more information.

Stack Overflow Post #1

Stack Overflow Post #2

Strongly Connected Components An implementation of Tarjan’s strongly connected components algorithm which uses this graph representation.

graph.p

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1: Count Even Digits Number

You are given an array of positive integers, @ints. Write a script to find out how many integers have even number of digits.

The majory of the work can be done in a single line. Conveniently the tr function returns the number of characters effected by the command. For our purposes that means telling tr to delete all numerals. We then check if the number of numerals removed is even inside of a grep block. The number of matches is then returned. Note the one catch, in order to use tr we need to assign $_ to a temporary value, $x. Otherwise we would get an error Modification of a read-only value.

The rest of the code just tests this function.

Sample Run

$ perl perl/ch-1.pl 
3 
0 
1
    

Part 2: Sum of Values

You are given an array of integers, @int and an integer $k. Write a script to find the sum of values whose index binary representation has exactly $k number of 1-bit set.

First, let’s concern ourselves with counting set bits. Here we can re-use some code that we’ve used before. This is a pretty standard way to count bits. This procedure is to do a bitwise AND operation for the least significant bit and check if it is set. We then right shift and repeat until no bits remain. This code is actually a modification of code used in TWC 079!

With that necessary work taken care of we need to loop over the given array of integers and (1) check to see if the index contains the correct number of set bits and, if that is the case, add to the rolling sum. Finally, return the sum.

The rest of the code drives some tests.

Sample Run

$ perl perl/ch-2.pl 
17 
11 
2
    

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two array of languages and its popularity. Write a script to sort the language based on popularity.

Solution

make_pairs(K, V, K-V).

sort_language(Languages, Popularity, SortedLanguages):-
    maplist(make_pairs, Popularity, Languages, PopularityLanguages),
    keysort(PopularityLanguages, SortedPopularityLanguages),
    findall(Language,  member(_-Language, SortedPopularityLanguages), SortedLanguages).

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- sort_language([2, 1, 3], [perl, c, python], SortedLanguages). 

SortedLanguages = [1,2,3]

yes
| ?- 

Notes

A pretty standard Prolog convention is the - separated Pair. So here all we need do is generate the pairs of popularity and language, and then use keysort/2 to get everything in the right order.

Part 2

You are given an array of integers >= 0. Write a script to return the largest number formed by concatenating some of the given integers in any order which is also multiple of 3. Return -1 if none found.

Solution

largest_of_three(Numbers, LargestOfThree):-
    findall(Number,(
        sublist(SubList, Numbers),
        \+ SubList = [],
        permutation(SubList, SubListPermutation),
        number_codes(Number, SubListPermutation),
        0 is Number mod 3), NumbersOfThree),
    ((NumbersOfThree = [], LargestOfThree = -1);
     (max_list(NumbersOfThree, LargestOfThree))). 

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- largest_of_three("819", LargestOfThree).

LargestOfThree = 981

yes
| ?- largest_of_three("86710", LargestOfThree).

LargestOfThree = 8760

(1 ms) yes
| ?- largest_of_three("1", LargestOfThree).    

LargestOfThree = -1 ? 

yes
| ?- 

Notes

This is perhaps the most naive solution to the problem: generate sublists and sort the matching permutations of those sublists.

References

Challenge 245

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two array of languages and its popularity. Write a script to sort the language based on popularity.

Solution

use Thread;
sub sort_language{
    my @language = @{$_[0]};
    my @popularity = @{$_[1]};
    my @threads;
    do{
        push @threads, Thread->new(
            sub{sleep($popularity[$_]); say $language[$_]}
        );
    } for 0 .. @popularity - 1;
    do{$_ -> join()} for @threads;
}

MAIN:{
    sort_language [qw/perl c python/], [2, 1, 3];
}

Sample Run

$ perl perl/ch-1.pl 
c
perl
python

Notes

This is the most ridiculous solution I could imagine for this problem! The sorting by popularity is done by way of a Sleep Sort. Sleep Sort is a very silly thing where you sleep for the values being sorted and then as the sleeps finish the solution comes together.

For added fun I used Perl's threading mechanism. A convenient wrapper for Perl's threads (which are properly called iThreads, and are basically the same construct as, say, JavaScript's workers) is use Thread which used to be an entirely different sort of threading model but is now just a handy set of functions around the current model. Be sure to read the documentation before using, for simple thread tasks it is perfectly fine! Just be aware of any issues with data sharing between threads, which is of no concern to us here.

For each array element of @popularity we create a new thread which is then pushed into an array for tracking all the threads we create. Each thread does nothing more than sleep and then print the corresponding language. Note that we do need to administer our threads in the end by looping over them and executing a join() to ensure they complete properly. We could just skip that, but doing so will cause Perl to warn us that not all threads may have properly completed, although in this case we wouldn't necessarily care since the program has completed executing anyway. Still, it's better to maintain the good practice of making sure everything is cleaned up!

Sleep Sort was the subject of a previous challenge

Part 2

You are given an array of integers >= 0. Write a script to return the largest number formed by concatenating some of the given integers in any order which is also multiple of 3. Return -1 if none found.

Solution

use v5.38;
use Algorithm::Permute;
sub largest_of_three{
    my @digits = @_;
    my $largest = -1;
    do{
        my $indices = $_;
        my @sub_digits = @digits[grep{vec($indices, $_, 1) == 1} 0 .. @digits - 1];
        my $permutor = Algorithm::Permute->new([@sub_digits]);
        while(my @permutation = $permutor->next()){
            my $d = join q//, @permutation;
            $largest = $d if $d > $largest && $d % 3 == 0;
        }
    } for 1 .. 2**@digits - 1;
    return $largest;
}

MAIN:{
    say largest_of_three 8, 1, 9;
    say largest_of_three 8, 6, 7, 1, 0;
    say largest_of_three 1;
}

Sample Run

$ perl perl/ch-2.pl 
981
8760
-1

Notes

I am not sure I have a whole lot to write about this one! My approach here is to take sublists and permute each one, checking at each step for divisibility by three. This works very well for small sets of digits but I cannot think of a more scaleable solution. Suppose we are given a million digits, is it possible to make some statement on the size of the number of digits we can use to compose a number as required? I suspect this problem is hitting on deeper complexities than I considered at first.

References

Thread

Sleep Sort

Challenge 245

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of integers. Write a script to calculate the number of integers smaller than the integer at each index.

Solution

smaller([], _, 0).
smaller([H|Integers], X, Y):-
    smaller(Integers, X, Y0),
    ((X > H, succ(Y0, Y));
     (X =< H, Y = Y0)).

count_smaller(Integers, CountSmaller):-
    maplist(smaller(Integers), Integers, CountSmaller).

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- count_smaller([2, 2, 2], CountSmaller). 

CountSmaller = [0,0,0]

yes
| ?- count_smaller([6, 5, 4, 8], CountSmaller).

CountSmaller = [2,1,0,3] ? 

yes
| ?- count_smaller([8, 1, 2, 2, 3], CountSmaller).

CountSmaller = [4,0,1,1,3] ? 

yes
| ?- 

Notes

Probably this is the most obvious way to count up smaller elements as required. In order to cut down on the recursion I call smaller/3 via a maplist/3.

Part 2

You are given an array of integers representing the strength. Write a script to return the sum of the powers of all possible combinations; power is defined as the square of the largest number in a sequence, multiplied by the smallest.

Solution

group_hero(Group, GroupHero):-
    findall(Hero, (
        sublist(SubList, Group),
        max_list(SubList, Maximum),
        min_list(SubList, Minimum),
        Hero #= Maximum**2 * Minimum
    ), Heroes),
    sum_list(Heroes, GroupHero). 

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- group_hero([2, 1, 4], GroupHero).

GroupHero = 141

yes
| ?-

Notes

The core of this problem is to enumerate all the Power Sets of the Group list. In other programming languages enumerating all sublists of a list is straightforward enough, but requires much more code. Here, with Prolog, we need only call sublist/2 with backtracking. We use a findall/3 to generate all the necessary backtracking and create the list of intermediate sums, which are then all summed for the final solution.

References

Challenge 244

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of integers. Write a script to calculate the number of integers smaller than the integer at each index.

Solution

use v5.38;
sub count_smaller{
    my @integers = @_;
    my @integers_sorted = sort {$a <=> $b} @integers;
    return map {  
        my $x = $_;
        (grep { $integers[$x] == $integers_sorted[$_]} 0 .. @integers_sorted - 1)[0];
    } 0 .. @integers - 1;
}

MAIN:{
    say join q/, /, count_smaller qw/8 1 2 2 3/;
    say join q/, /, count_smaller qw/6 5 4 8/;
    say join q/, /, count_smaller qw/2 2 2/;
}

Sample Run

$ perl perl/ch-1.pl 
4, 0, 1, 1, 3
2, 1, 0, 3
0, 0, 0

Notes

I'll admit this is a little convoluted. Since we already have a nested loop with the map and grep this is not any more efficient than if I had just searched and summed the smaller elements.

The idea here is to sort the array of integers and then for each element in the original array find it's position in the sorted array. The number of elements preceding the sought after element in the sorted list are the number of elements which are smaller than it.

This approach may have a performance benefit in the case of extremely large lists coupled with early termination of the inner loop.

Part 2

You are given an array of integers representing the strength. Write a script to return the sum of the powers of all possible combinations; power is defined as the square of the largest number in a sequence, multiplied by the smallest.

Solution

use v5.38;
sub group_hero{
    my @group = @_;
    my $group_hero = 0;
    do{
        my $indices = $_;
        my @hero = sort {$a <=> $b} @group[grep{vec($indices, $_, 1) == 1} 0 .. @group - 1];
        $group_hero += ($hero[@hero - 1]**2 * $hero[0]);
    } for 1 .. 2**@group - 1;
    return $group_hero;
}

MAIN:{
    say group_hero qw/2 1 4/;
}

Sample Run

$ perl perl/ch-2.pl 
141

Notes

A core part of this problem is to compute the Power Set, set of all subsets, of the original array. To do this we use the well known trick of mapping the set bits of the numbers from 1 .. N^2, where N is the size of the array, to the array indices.

@group[grep{vec($indices, $_, 1) == 1} 0 .. @group - 1] examines which bit within each number $_ in 1 .. 2**@group - 1 are set and then uses them as the indices to @group. The elements from within @group that are found this way are then sorted to obtain the maximum and minimum needed for the final calculation.

References

Power Set

Challenge 244

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of integers. Write a script to return the number of reverse pairs in the given array.

Solution

reverse_pair(X, Y, Z):-
    (X =\= Y, X > Y + Y, Z = 1, !); Z = 0.
reverse_pairs([], 0).    
reverse_pairs([H|T], ReversePairs):-
    reverse_pairs(T, R),
    maplist(reverse_pair(H), T, RP),
    sum_list(RP, Sum),
    ReversePairs is R + Sum.  

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- reverse_pairs([1, 3, 2, 3, 1], ReversePairs).  

ReversePairs = 2

yes
| ?- reverse_pairs([2, 4, 3, 5, 1], ReversePairs).  

ReversePairs = 3

yes
| ?- 

Notes

reverse_pair/3 implements the reverse pair criteria and is called via a maplist/3 in reverse_pairs/3 which recurses over the list and counts up all Reverse Pairs found.

Part 2

You are given an array of positive integers (>=1). Write a script to return the floor sum.

Solution

floor_sum_pair(X, Y, Z):-
    Z is floor(X / Y).

floor_sum(Integers, FloorSum):-
    floor_sum(Integers, Integers, FloorSum).
floor_sum([], _, 0).    
floor_sum([H|T], L, FloorSum):-
    floor_sum(T, L, F),
    maplist(floor_sum_pair(H), L, FS),
    sum_list(FS, Sum),
    FloorSum is F + Sum.  

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- floor_sum([2, 5, 9], FloorSum).

FloorSum = 10

yes
| ?- floor_sum([7, 7, 7, 7, 7, 7, 7], FloorSum).

FloorSum = 49

(1 ms) yes
| ?- 

Notes

The process here is, co-incidentally, much the same as the first part above. We recurse over the list and use a maplist/3 to build an incremental sum at each step.

References

Challenge 243

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of integers. Write a script to return the number of reverse pairs in the given array.

Solution

use v5.38;
sub reverse_pairs{
    my @integers = @_;
    my @reverse_pairs;
    do{
        my $i = $_;
        do{
            my $j = $_;
            push @reverse_pairs, [$i, $j] if $integers[$i] > $integers[$j] + $integers[$j];
        } for $i + 1 .. @integers - 1;
    } for 0 .. @integers - 1;
    return 0 + @reverse_pairs;
}

MAIN:{
    say reverse_pairs 1, 3, 2, 3, 1;
    say reverse_pairs 2, 4, 3, 5, 1;
}

Sample Run

$ perl perl/ch-1.pl 
2
3

Notes

A reverse pair is a pair (i, j) where:

a) 0 <= i < j < nums.length 

and

b) nums[i] > 2 * nums[j].

I've been on a bit of a recursion kick recently, but I didn't have the appetite for it this week. A nested loop and we're done!

Part 2

You are given an array of positive integers (>=1). Write a script to return the floor sum.

Solution

use v5.38;
use POSIX;
sub floor_sum{
    my @integers = @_;
    my $floor_sum;
    do{
        my $i = $_;
        do{
            my $j = $_;
            $floor_sum += floor($integers[$i] / $integers[$j]);
        } for 0 .. @integers - 1;
    } for 0 .. @integers - 1;
    return $floor_sum;
}

MAIN:{
    say floor_sum 2, 5, 9;
    say floor_sum 7, 7, 7, 7, 7, 7, 7;
}

Sample Run

$ perl perl/ch-2.pl 
10
49

Notes

See above comment about not being as recursive this week!

References

Challenge 243

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two arrays of integers. Write a script to find out the missing members in each other arrays.

Solution

missing(L, E, Member):-
    (member(E, L), Member = nil);
    (\+ member(E, L), Member = E).
missing_members([List1, List2], [Missing1, Missing2]):-
    maplist(missing(List2), List1, Missing1Nil),
    delete(Missing1Nil, nil, Missing1),
    maplist(missing(List1), List2, Missing2Nil),
    delete(Missing2Nil, nil, Missing2). 

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- missing_members([[1, 2, 3], [2, 4, 6]] ,Missing).

Missing = [[1,3],[4,6]] ? 

yes
| ?- missing_members([[1, 2, 3, 3], [1, 1, 2, 2]] ,Missing).

Missing = [[3,3],[]] ? 

yes
| ?- missing_members([[1, 2, 3, 3], [1, 1, 2, 2]], Missing), maplist(sort, Missing, MissingNoDuplicates). 

Missing = [[3,3],[]]
MissingNoDuplicates = [[3],[]] ? 

yes
| ?- 

Notes

missing/3 is used in a maplist/3 to determine which elements are missing from an array. If they are not missing a nil is set for it. By deleting the nil elements all that remain are the ones that are missing. This solution doesn't itself remove duplicate missing elements that are identified. That said, as you can see in the example above that can be added, say, using sort/2.

Part 2

You are given n x n binary matrix. Write a script to flip the given matrix as below.

Solution

flip(B, F):-
    F is \ B /\ 1.
flip_matrix([], []).    
flip_matrix([Row|Matrix], [RowFlipped|MatrixFlipped]):-
    reverse(Row, RowReversed),
    maplist(flip, RowReversed, RowFlipped),
    flip_matrix(Matrix, MatrixFlipped).

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- flip_matrix([[1, 1, 0], [1, 0, 1], [0, 0, 0]], FlippedMatrix).

FlippedMatrix = [[1,0,0],[0,1,0],[1,1,1]]

yes
| ?- flip_matrix([[1, 1, 0, 0], [1, 0, 0, 1], [0, 1, 1, 1], [1, 0, 1, 0]], FlippedMatrix).

FlippedMatrix = [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]

yes
| ?- 

Notes

For the given matrix we need only recursively consider each row, reverse it, do the necessary bit flips, and then assemble the newly flipped rows into the completed Flipped Matrix.

References

Challenge 242

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two arrays of integers. Write a script to find out the missing members in each other arrays.

Solution

use v5.38;
use boolean;
use Data::Dump q/pp/;
sub missing_members{
    my @r;
    my($a0, $a1) = @_;
    my $missing0 = [];
    missing_members_r([@{$a0}], [@{$a1}], $missing0);
    my $missing1 = [];
    missing_members_r([@{$a1}], [@{$a0}], $missing1);
    push @r, $missing0 if @{$missing0} > 0;
    push @r, $missing1 if @{$missing1} > 0;
    return @r;
}

sub missing_members_r{
    my($a0, $a1, $missing, $seen) = @_;
    $seen = [] if !defined($seen);
    my $x = shift @{$a0};
    push @{$missing}, $x if missing_r($x, [@{$a1}]) && !seen_r($x, $seen); 
    push @{$seen}, $x;
    missing_members_r($a0, $a1, $missing, $seen) if @{$a0} > 0;
}

sub missing_r{
    my($x, $a0) = @_;
    return true if @{$a0} == 0;
    if(@{$a0}){
        my $y = shift @{$a0};
        if($x == $y){ 
            return false;
        }
    }
    return missing_r($x, $a0);
}

sub seen_r{
    my($x, $seen) = @_;
    return false if @{$seen} == 0;
    my $y = shift @{$seen};
    if($x == $y){
        return true;
    }
    return seen_r($x, $seen);
}

MAIN:{
    my @array1 = (1, 2, 3);
    my @array2 = (2, 4, 6);
    say pp missing_members \@array1, \@array2;
    @array1 = (1, 2, 3, 3);
    @array2 = (1, 1, 2, 2);
    say pp missing_members \@array1, \@array2;
}

Sample Run

$ perl perl/ch-1.pl 
([1, 3], [4, 6])
[3]

Notes

So, yeah, this could just be a nice quick use of grep, but where is the fun in that!?!? Just looping over the arrays is not that exciting of an alternative, what other options are there? I know, how about a whole lot of recursion! That was pretty much my thought process here.

Really, all this code is doing is looping over the two arrays and looking for which elements are not contained in each. The looping, such as it is, happens recursively in missing_members_r() and missing_r(). Duplicates are possible and we avoid these, again recursively, using seen_r() rather than, say, grep or hash keys.

Part 2

You are given n x n binary matrix. Write a script to flip the given matrix as below.

Solution

use v5.38;
use Data::Dump q/pp/;
sub flip_matrix{
    return map { 
        my $row = $_;
        [map {~$_ & 1} reverse @{$row}]
    } @_;
}

MAIN:{
    my @matrix = ([1, 1, 0], [1, 0, 1], [0, 0, 0]);
    say pp flip_matrix @matrix;
    @matrix = ([1, 1, 0, 0], [1, 0, 0, 1], [0, 1, 1, 1], [1, 0, 1, 0]);
    say pp flip_matrix @matrix;
}

Sample Run

$ perl perl/ch-2.pl 
([1, 0, 0], [0, 1, 0], [1, 1, 1])
([1, 1, 0, 0], [0, 1, 1, 0], [0, 0, 0, 1], [1, 0, 1, 0])

Notes

After all the recursive exitment in part 1 of this week's challenge I just went with a quick nested map for part 2.

References

Challenge 242

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array (3 or more members) of integers in increasing order and a positive integer. Write a script to find out the number of unique Arithmetic Triplets satisfying the given rules.

Solution

arithmetic_triplets(Numbers, Difference, TripletCount):-
    length(Triplet, 3),  
    member(I, Triplet),      
    member(J, Triplet),      
    member(K, Triplet),      
    fd_domain(Triplet, Numbers),  
    fd_all_different(Triplet), 
    Difference #= J - I,
    Difference #= K - J,  
    I #< J,
    J #< K,
    findall(Triplet, fd_labeling(Triplet), Triplets),
    length(Triplets, TripletCount).  

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- arithmetic_triplets([0, 1, 4, 6, 7, 10], 3, TripletCount).

TripletCount = 2 ? 

yes
| ?- arithmetic_triplets([4, 5, 6, 7, 8, 9], 2, TripletCount). 

TripletCount = 2 ? 

yes
| ?- 

Notes

The rules for arithmetic triples are a) i < j < k b) nums[j] - nums[i] == diff and c) nums[k] - nums[j] == diff, where diff is a provided parameter. The code above implements these rules directly, letting Prolog do all the work for us!

Part 2

You are given an array of unique positive integers greater than 2. Write a script to sort them in ascending order of the count of their prime factors, tie-breaking by ascending value.

Solution

prime_factors(N, L):- 
    N > 0,  
    prime_factors(N, L, 2).
prime_factors(1, [], _):- 
    !.
prime_factors(N, [F|L], F):-                     
    R is N // F, 
    N =:= R * F, 
    !, 
    prime_factors(R, L, F).
prime_factors(N, L, F):-
    next_factor(N, F, NF), 
    prime_factors(N, L, NF).
next_factor(_, 2, 3):- 
    !.
next_factor(N, F, NF):- 
    F * F < N, 
    !, 
    NF is F + 2.
next_factor(N, _, N).

kvf_insert_sort(List,Sorted):-
    i_sort(List,[],Sorted).

i_sort([],Acc,Acc).
i_sort([H|T],Acc,Sorted):-
    kvf_insert(H,Acc,NAcc),
    i_sort(T,NAcc,Sorted).

kvf_insert(K0-V0,[K1-V1|T],[K1-V1|NT]):-
    V0 > V1,
    kvf_insert(K0-V0,T,NT).
kvf_insert(K0-V0,[K1-V1|T],[K0-V0,K1-V1|T]):-
    V0 < V1.
kvf_insert(K0-V0,[K1-V1|T],[K1-V1|NT]):-
    V0 = V1,
    K0 > K1,
    kvf_insert(K0-V0,T,NT).
kvf_insert(K0-V0,[K1-V1|T],[K0-V0,K1-V1|T]):-
    V0 = V1,
    K0 < K1.    
kvf_insert(K0-V0, [], [K0-V0]).

write_factor_sorted([K-_|[]]):-
    write(K),
    nl.
write_factor_sorted([K-_|T]):-
    write(K),
    write(', '),
    write_factor_sorted(T).

factor_counter(Number, Number-FactorCount):-
    prime_factors(Number, Factors),
    length(Factors, FactorCount).

factor_sorter(Numbers, FactorsSorted):-
    maplist(factor_counter, Numbers, Factors),
    kvf_insert_sort(Factors, FactorsSorted).

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- factor_sorter([11, 8, 27, 4], FactorsSorted), write_factor_sorted(FactorsSorted).
11, 4, 8, 27

FactorsSorted = [11-1,4-2,8-3,27-3] ? 

yes
| ?- 

Notes

This code is build mainly from pieces from previous challenges. The prime factorization code is something I've used several times and the modified Insertion Sort is a minor modification of code from TWC 233.

References

Challenge 241

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array (3 or more members) of integers in increasing order and a positive integer. Write a script to find out the number of unique Arithmetic Triplets satisfying the given rules.

Solution

use v5.38;
sub arithmetic_triplets{
    my $counter = 0;
    my $difference = shift;
    arithmetic_triplets_r($difference, \$counter, [@_[0 .. @_ -1]], [@_[1 .. @_ -1]], [@_[2 .. @_ -1]]);   
    return $counter;
} 

sub arithmetic_triplets_r{
    my $difference = $_[0]; 
    my $counter = $_[1]; 
    my @i = @{$_[2]};         
    my @j = @{$_[3]};         
    my @k = @{$_[4]};        
    if(@i > 0 && @j > 0 && @k > 0){
        $$counter++ if $j[0] - $i[0] == $difference && $k[0] - $j[0] == $difference;   
        arithmetic_triplets_r($difference, $counter, [@i], [@j], [@k[1 .. @k - 1]]);   
    }
    elsif(@i > 0 && @k == 0 && @j > 0){
        arithmetic_triplets_r($difference, $counter, [@i], [@j[1 .. @j - 1]], [@j[2 .. @j - 1]]);   
    }
    elsif(@i > 0 && @k == 0 && @j == 0){
        arithmetic_triplets_r($difference, $counter, [@i[1 .. @i - 1]], [@i[2 .. @i - 1]], [@i[3 .. @i - 1]]);   
    }
}

MAIN:{
    my $difference;
    $difference = 3;
    say arithmetic_triplets $difference, 0, 1, 4, 6, 7, 10;
    $difference = 2;
    say arithmetic_triplets $difference, 4, 5, 6, 7, 8, 9;  
}

Sample Run

$ perl perl/ch-1.pl 
2
2

Notes

The rules for arithmetic triples are a) i < j < k b) nums[j] - nums[i] == diff and c) nums[k] - nums[j] == diff, where diff is a provided parameter. The code above implements these rules somewhat in the obvious way, looping thricely over the list, but recursively.

Part 2

You are given an array of unique positive integers greater than 2. Write a script to sort them in ascending order of the count of their prime factors, tie-breaking by ascending value.

Solution

use v5.38;
sub prime_factor{
    my $x = shift(@_); 
    my @factors;    
    for (my $y = 2; $y <= $x; $y++){
        next if $x % $y;
        $x /= $y;
        push @factors, $y;
        redo;
    }
    return @factors;  
}

sub prime_order{
    my %factor_i = map{($_, 0 + prime_factor($_))} @_;
    my $factor_sorter = sub{
        my $c = $factor_i{$a} <=> $factor_i{$b};
        return $c unless !$c;
        return $a <=> $b;
    };
    return sort $factor_sorter @_;
}

MAIN:{
     say join q/, /, prime_order 11, 8, 27, 4;
}

Sample Run

$ perl perl/ch-2.pl 
11, 4, 8, 27

Notes

This code borrows from two previous challenges: The prime factor code has been used several times, but in this case I referred to the Attractive Number challenge from TWC 041. The sorting is a variant of the frequency sort from TWC 233. If you write enough code you don't need GitHub Copilot, you can just re-use your own work!

References

Challenge 241

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of strings and a check string. Write a script to find out if the check string is the acronym of the words in the given array.

Solution

acronym(Strings, CheckString):-
    maplist(nth(1), Strings, CheckStringUpperCaseCodes),
    maplist(char_code, CheckStringUpperCase, CheckStringUpperCaseCodes),
    maplist(lower_upper, CheckStringLowerCase, CheckStringUpperCase),
    atom_chars(CheckStringA, CheckStringLowerCase),
    atom_codes(CheckStringA, CheckString).

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- acronym(["Perl", "Python", "Pascal"], "ppp"). 

true ? 

yes
| ?- acronym(["Perl", "Raku"], "rp").             

no
| ?- acronym(["Oracle", "Awk", "C"], "oac").

true ? 

yes
| ?- acronym(["Oracle", "Awk", "C"], A), atom_codes(Acronym, A).

A = [111,97,99]
Acronym = oac ? 

yes
| ?- 

Notes

In keeping with the spirit of the original, Perl centric, challenge question I use strings instead of Prolog atoms. The difference is that strings will be represented as lists of character codes, so a little extra code is required.

Chanelling the spirit of Prolog, the solution will backtrack and provide the acronym if that variable is given uninstantiated!

Part 2

You are given an array of integers. Write a script to create an array such that new[i] = old[old[i]] where 0 <= i < new.length.

Solution

build_list(_, [], []).
build_list(Old, [OldH|OldT], [NewH|NewT]):-
    succ(OldH, I),
    nth(I, Old, NewH),
    build_list(Old, OldT, NewT).

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- Old = [0, 2, 1, 5, 3, 4], build_list(Old, Old, New).

New = [0,1,2,4,5,3]
Old = [0,2,1,5,3,4] ? 

yes
| ?- Old = [5, 0, 1, 2, 3, 4], build_list(Old, Old, New).

New = [4,5,0,1,2,3]
Old = [5,0,1,2,3,4] ? 

yes
| ?- 

Notes

This is basically the same recursive procedure as used in the Perl solution to the same problem. I did the Perl version first, which was helpful to prototype the recursion.

References

Challenge 240

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of strings and a check string. Write a script to find out if the check string is the acronym of the words in the given array.

Solution

use v5.38;
use boolean;
sub acronym{
    my($strings, $acronym) = @_;
    return boolean(join(q//, map {(split //, lc $_)[0]} @{$strings}) eq lc $acronym);
}

MAIN:{
    say acronym [qw/Perl Python Pascal/], q/ppp/;
    say acronym [qw/Perl Raku/], q/rp/;
    say acronym [qw/Oracle Awk C/], q/oac/;
}

Sample Run

$ perl perl/ch-1.pl 
1
0
1

Notes

I really wracked my brain to try and come up with a simpler solution and I couldn't!

Part 2

You are given an array of integers. Write a script to create an array such that new[i] = old[old[i]] where 0 <= i < new.length.

Solution

use v5.38;
sub build_array{ 
    push @{$_[0]}, $_[$_[@{$_[0]} + 1] + 1];
    return $_[0] if @{$_[0]} == @_ - 1;
    goto __SUB__;
}

MAIN:{
    say join q/, /, @{build_array([], 0, 2, 1, 5, 3, 4)};
    say join q/, /, @{build_array([], 5, 0, 1, 2, 3, 4)};
}

Sample Run

$ perl perl/ch-2.pl 
0, 1, 2, 4, 5, 3
4, 5, 0, 1, 2, 3

Notes

First off, yes, this code is a bit obfuscated! Writing obfuscated code is not usually something I strive to do, but I was sort of forced down this road. See, what happened is that I read E. Choroba's solution on Discord despite the spoiler warnings! Now, I didn't want his solution to influence mine so I forced myself to come up with something which would be as different as possible.

build_array uses recursion to accumulate the result in the first argument, an array reference. We use the length of the array reference as the index used to look up, and assign elements, from the original array. The original array is present as all remaining arguments in the subroutine call, so we'll need to adjust the indices by 1 to allow for the array reference accumulator as the first argument. The recursion is created using goto __SUB__ which by default retains the original array arguments. Since our accumulator is an array reference and none of the other arguments change then we can make use of this as a convenience. The recursion ends when the accumulated array is of the same length as the original array, then we know that all elements have been processed.

References

Challenge 240

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two arrays of strings. Write a script to find out if the word created by concatenating the array elements is the same.

Solution

concatenate_all([], '').
concatenate_all([H|T], Concatenated):-
    concatenate_all(T, C),
    atom_concat(H, C, Concatenated).

same_string(L0, L1):-
    concatenate_all(L0, C0),
    concatenate_all(L1, C1),
    C0 == C1. 

Sample Run

% gprolog --consult-file prolog/ch-1.p
| ?- same_string([ab, c], [a, bc]).

yes
| ?- same_string([ab, c], [ac, b]). 

no
| ?- same_string([ab, cd, e], [abcde]).

yes
| ?- 

Notes

The problem is given as strings, which I interpret here as meaning atoms, in which case we need to concatenate all the atoms together and then check to see if they are equal.

If, instead, I had strictly used strings (arrays of character codes) then there would be no need to actually concatenate anything. In that case we could just flatten the lists and then check to see if the lists were the same.

Part 2

You are given an array of strings and allowed string having distinct characters. A string is consistent if all characters in the string appear in the string allowed. Write a script to return the number of consistent strings in the given array.

Solution

consistent(Allowed, String, Consistent):-
    subtract(String, Allowed, Subtracted),
    length(Subtracted, SubtractedLength),
    ((SubtractedLength == 0, Consistent = 1);
     (SubtractedLength == 1, Consistent = 0)).

consistent_strings(Strings, Allowed, ConsistentStringsCount):-
    maplist(consistent(Allowed), Strings, ConsistentStrings),
    sum_list(ConsistentStrings, ConsistentStringsCount).

Sample Run

% gprolog --consult-file prolog/ch-2.p 
| ?- consistent_strings(["ad", "bd", "aaab", "baa", "badab"], "ab", ConsistentStrings).

ConsistentStrings = 2 ? 

(1 ms) yes
| ?- consistent_strings(["a", "b", "c", "ab", "ac", "bc", "abc"], "abc", ConsistentStrings).

ConsistentStrings = 7 ? 

yes
| ?- consistent_strings(["cc", "acd", "b", "ba", "bac", "bad", "ac", "d"], "cad", ConsistentStrings).

ConsistentStrings = 4 ? 

yes
| ?- 

Notes

Here I count up all the consistent strings by using a maplist/3 to create a list of 0s and 1s. 0 if the string is not consistent, 1 if it is consistent. The check for if a string is consistent is done in a helper predicate which works by removing all the allowed characters and then checking if all characters have been removed, which satisfies the criteria.

References

Challenge 239

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given two arrays of strings. Write a script to find out if the word created by concatenating the array elements is the same.

Solution

use v5.36;
use boolean;
sub same_string{
    my($a1, $a2) = @_;
    return boolean(join(q//, @{$a1}) eq join(q//, @{$a2}));
}

MAIN:{
    say same_string [qw/ab c/], [qw/a bc/];
    say same_string [qw/ab c/], [qw/ac b/];
    say same_string [qw/ab cd e/], [qw/abcde/];
}

Sample Run

$ perl perl/ch-1.pl 
1
0
1

Notes

I really wracked my brain to try and come up with a simpler solution and I couldn't!

Part 2

You are given an array of strings and allowed string having distinct characters. A string is consistent if all characters in the string appear in the string allowed. Write a script to return the number of consistent strings in the given array.

Solution

use v5.36;
sub is_consistent{
    my($s, $allowed) = @_;
    $s =~ s/[$allowed]//g;
    return $s eq q//;
}

sub consistent_strings{
    my($strings, $allowed) = @_;
    my @consistent = grep { is_consistent $_, $allowed } @{$strings};
    return 0 + @consistent;
}

MAIN:{
    say consistent_strings [qw/ad bd aaab baa badab/], q/ab/; 
    say consistent_strings [qw/a b c ab ac bc abc/], q/abc/; 
    say consistent_strings [qw/cc acd b ba bac bad ac d/], q/cad/;
}

Sample Run

$ perl perl/ch-2.pl 
2
7
4

Notes

To check if a string is consistent using the given definition, all the allowed characters are removed from the given string. If the result is the empty string then we know the string meets the requirements. Here this is broken out to the is_consistent function. That in turn is called from within a grep which checks the entire list of strings.

References

Challenge 239

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are asked to sell juice each costs $5. You are given an array of bills. You can only sell ONE juice to each customer but make sure you return exact change back. You only have $5, $10 and $20 notes. You do not have any change in hand at first. Write a script to find out if it is possible to sell to each customers with correct change.

Solution

use v5.38;
use boolean;
use constant COST_JUICE => 5;

sub exact_change{
    my @bank;
    my $current_customer = shift;
    { 
        push @bank, $current_customer if $current_customer == COST_JUICE;
        if($current_customer > COST_JUICE){
            my $change_due = $current_customer - COST_JUICE;
            my @bank_sorted = sort {$a <=> $b} @bank;
            my @bank_reserved;
            {
                my $bill = pop @bank_sorted;
                push @bank_reserved, $bill if $change_due < $bill;
                $change_due -= $bill if $change_due >= $bill;
                redo if @bank_sorted;
            } 
            return false if $change_due != 0;
            @bank = @bank_reserved;
            push @bank, $current_customer;
        }
        $current_customer = shift; 
        redo if $current_customer;
    }
    return true;
}


MAIN:{
    say exact_change 5, 5, 5, 10, 20;
    say exact_change 5, 5, 10, 10, 20;
    say exact_change 5, 5, 5, 20;
}

Sample Run

$ perl perl/ch-1.pl 
1
0
1

Notes

Making change is easy as long as we preferentially use larger bills first. To do so all we need to do is sort any accumulated payments and then pop off the change as required by the current transaction, if possible.

Part 2

You are given an array of unique integers. Write a script to determine how many loops are in the given array. To determine a loop: Start at an index and take the number at array[index] and then proceed to that index and continue this until you end up at the starting index.

Solution

use v5.38;
use boolean;
sub loop_counter{
    my @integers = @_;
    my @loops;
    do{
        my @loop;
        my $loop_found = false;
        my $start = $_;
        my $next = $integers[$start];
        push @loop, $start, $next;
        my $counter = 1;
        {
            if($next == $start){
                shift @loop;
                if(@loops == 0 || @loop == 2){
                    push @loops, \@loop;
                    my @loop;
                    $loop_found = true;
                }
                else{
                    my $loop_duplicate = false;
                    my @s0 = sort @loop;
                    do { 
                        my @s1 = sort @{$_};                        
                        $loop_duplicate = true if((@s0 == @s1) && (0 < grep {$s0[$_] == $s1[$_]} 0 .. @s0 - 1));
                    } for @loops;   
                    if(!$loop_duplicate){
                        $loop_found = true;
                        push @loops, \@loop;
                    }
                    else{
                        $counter = @integers + 1; 
                    }           
                }
            }
            else{
                $next = $integers[$next];
                push @loop, $next;   
                $counter++;     
            }
            redo unless $loop_found || $counter > @integers;
        }
    } for 0 .. @integers - 1; 
    return @loops + 0;
}

MAIN:{
    say loop_counter 4, 6, 3, 8, 15, 0, 13, 18, 7, 16, 14, 19, 17, 5, 11, 1, 12, 2, 9, 10;
    say loop_counter 0, 1, 13, 7, 6, 8, 10, 11, 2, 14, 16, 4, 12, 9, 17, 5, 3, 18, 15, 19;
    say loop_counter 9, 8, 3, 11, 5, 7, 13, 19, 12, 4, 14, 10, 18, 2, 16, 1, 0, 15, 6, 17;
}

Sample Run

$ perl perl/ch-2.pl 
3
6
1

Notes

When I first approached this problem I didn't appreciate that many loops are just cycles of each other. In those cases we need to identify if such cyclical duplicates exit. Much of the code here, then, is for examining such cases. The detection is done by comparing each loop to the existing loops, in sorted order. if there are any equivalents we know we have a duplicate.

The line shift @loop; is to remove to starting point, which is convenient to maintain up until storing in the @loops array.

References

Challenge 236

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of words made up of alphabets only. Write a script to find the number of pairs of similar words. Two words are similar if they consist of the same characters.

Solution

similar(A, B, Similar):-
    atom_codes(A, ACodes),
    sort(ACodes, ASorted),
    atom_codes(B, BCodes),
    sort(BCodes, BSorted),
    (ASorted = BSorted, Similar = 1);
    Similar = 0.

count_similar_pairs([], 0).
count_similar_pairs([Word|Words], PairsSimilar):-
    count_similar_pairs(Words, P), 
    maplist(similar(Word), Words, Similar), !,
    sum_list(Similar, SimilarCount),
    PairsSimilar is P + SimilarCount.

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- count_similar_pairs([aba, aabb, abcd, bac, aabc], PairsSimilar).

PairsSimilar = 2

yes
| ?- count_similar_pairs([aabb, ab, ba], PairsSimilar).              

PairsSimilar = 3

(1 ms) yes
| ?- count_similar_pairs([nba, cba, dba], PairsSimilar).             

PairsSimilar = 0

yes
| ?- 

Notes

Similarity of words is determined by doing a pairwise comparison of the unique character codes. I've gotten into the habit of counting things by using maplist with a predicate that provides a list of 0 and 1 elements. The count is done by summing the list. Here the counting is done in this way by similar/3. count_similar_pairs/2 recursively considers all pairs.

Part 2

You are given an array of integers. Write a script to sort the given array in increasing order based on the frequency of the values. If multiple values have the same frequency then sort them in decreasing order.

Solution

kvf_insert_sort(List,Sorted):-
    i_sort(List,[],Sorted).

i_sort([],Acc,Acc).
i_sort([H|T],Acc,Sorted):-
    kvf_insert(H,Acc,NAcc),
    i_sort(T,NAcc,Sorted).

kvf_insert(K0-V0,[K1-V1|T],[K1-V1|NT]):-
    V0 > V1,
    kvf_insert(K0-V0,T,NT).
kvf_insert(K0-V0,[K1-V1|T],[K0-V0,K1-V1|T]):-
    V0 < V1.
kvf_insert(K0-V0,[K1-V1|T],[K1-V1|NT]):-
    V0 = V1,
    K0 < K1,
    kvf_insert(K0-V0,T,NT).
kvf_insert(K0-V0,[K1-V1|T],[K0-V0,K1-V1|T]):-
    V0 = V1,
    K0 > K1.    
kvf_insert(K0-V0, [], [K0-V0]).

frequency_writer(_-0).
frequency_writer(K-F):-
    write(K),
    write(', '),
    succ(X, F),
    frequency_writer(K-X).

write_frequencies([K-F|[]]):-
    succ(X, F),
    frequency_writer(K-X),
    write(K),
    nl.
write_frequencies([H|T]):-
    frequency_writer(H),
    write_frequencies(T).

frequency_counter(Numbers, Number, Number-Count):-
    length(Numbers, StartCount),
    delete(Numbers, Number, NumberDeleted),
    length(NumberDeleted, EndCount),
    Count is StartCount - EndCount.

frequency_sorter(Numbers, FrequencySorted):-
    sort(Numbers, UniqueNumbers),
    maplist(frequency_counter(Numbers), UniqueNumbers, Frequencies),
    kvf_insert_sort(Frequencies, FrequencySorted).

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- frequency_sorter([1, 1, 2, 2, 2, 3], Sorted), write_frequencies(Sorted).
3, 1, 1, 2, 2, 2

Sorted = [3-1,1-2,2-3] ? 

(1 ms) yes
| ?- frequency_sorter([2, 3, 1, 3, 2], Sorted), write_frequencies(Sorted).
1, 3, 3, 2, 2

Sorted = [1-1,3-2,2-2] ? 

(1 ms) yes
| ?- frequency_sorter([-1, 1, -6, 4, 5, -6, 1, 4, 1], Sorted), write_frequencies(Sorted).
5, -1, 4, 4, -6, -6, 1, 1, 1

Sorted = [5-1,-1-1,4-2,-6-2,1-3] ? 

(1 ms) yes
| ?- 

Notes

First off, we get a count of the frequencies of each number in the list, via a maplist with frequency_counter/3. After that is when we hit the real complexity of the problem. This problem requires a somewhat unique idea of sorting frequencies! The frequencies have been built as key-value pairs but an ordinary sort or key sort won't work here for these unique requirements. All the required unique sort logic is contained in the kvf_insert_sort/2 and related predicates. This is a modification of insertion sort found in Roman Barták's Guide to Prolog Programming.

With the list of frequencies sorted all that is left is to print the result as specified, which is the work of write_frequencies/1. Those somewhat lengthy looking predicates expand the key-value pairs from the sorted result and print them in the new order.

References

Sort Algorithms in Prolog

Challenge 233

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of words made up of alphabets only. Write a script to find the number of pairs of similar words. Two words are similar if they consist of the same characters.

Solution

use v5.38;
use boolean;

sub is_similar{
    my($s0, $s1) = @_;
    my(%h0, %h1);
    do { $h0{$_} = undef } for split //, $s0; 
    do { $h1{$_} = undef } for split //, $s1; 
    return false if keys %h0 != keys %h1;
    do { return false if !exists $h1{$_} } for keys %h0;
    return true;
}

sub similar_words_pairs_count{
    my @words = @_;
    my @similar;
    do{
        my $word_index = $_;
        my @similar_temp = grep { $words[$word_index] ne $words[$_] && 
                                  is_similar $words[$word_index], $words[$_] } $word_index + 1 .. @words - 1;
        push @similar, @words[@similar_temp] if @similar_temp > 0;
    } for 0 .. @words - 1;
    return @similar + 0;
}

MAIN:{
    say similar_words_pairs_count qw/aba aabb abcd bac aabc/;
    say similar_words_pairs_count qw/aabb ab ba/;
    say similar_words_pairs_count qw/nba cba dba/;
}

Sample Run

$ perl perl/ch-1.pl 
2
3
0

Notes

The core of this problem is to count up the number of pairs of similar words. A clearly good use of grep, but how to do that exactly? Well, here we define a subroutine is_similar that returns a true/false value depending on if the words meet the definition of similar given in the problem. That's done by expanding the words into arrays of characters, stuffing those characters into hash key slots in order to force uniqueness, and then seeing if the two key sets are equal.

Once we have the logic to determine similarity worked out we can then use it in grep and count up the results.

Part 2

You are given an array of integers. Write a script to sort the given array in increasing order based on the frequency of the values. If multiple values have the same frequency then sort them in decreasing order.

Solution

use v5.38;
sub frequency_sort{
    my(@numbers) = @_;
    my %frequency;
    do{$frequency{$_}++} for @numbers;
    my $frequency_sorter = sub{
        my $c = $frequency{$a} <=> $frequency{$b};
        return $c unless !$c;
        return $b <=> $a;

    };
    return sort $frequency_sorter @numbers;
}

MAIN:{
    say join q/, /, frequency_sort 1, 1, 2, 2, 2, 3;
    say join q/, /, frequency_sort 2, 3, 1, 3, 2;
    say join q/, /, frequency_sort -1, 1, -6, 4, 5, -6, 1, 4, 1
}

Sample Run

$ perl perl/ch-2.pl 
3, 1, 1, 2, 2, 2
1, 3, 3, 2, 2
5, -1, 4, 4, -6, -6, 1, 1, 1

Notes

This problem ended up being a bit more complex than it seemed after the first reading. Perl makes this sort of complexity easy to manage though! sort can take a custom sorting subroutine as an argument. That is what is done here, with the requirements of the frequency sort for this problem implemented within the subroutine referenced by $frequency_sorter. This is written as an anonymous subroutine in order to obtain a closure around %frequency. Finally, observe that we can use the scalar reference directly with sort. sort is flexible enough to know how to use the reference.

References

Challenge 233

What's the Frequency, Kenneth?

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of distinct integers. Write a script to find all elements that is neither minimum nor maximum. Return -1 if you can’t.

Solution

not_min_max(Numbers, NotMinMax):-
    min_list(Numbers, Minimum),
    max_list(Numbers, Maximum),
    delete(Numbers, Minimum, NumbersNoMinimum),
    delete(NumbersNoMinimum, Maximum, NumbersNoMinimumNoMaximum),
    ((length(NumbersNoMinimumNoMaximum, 0), NotMinMax = -1), !;
     (NotMinMax = NumbersNoMinimumNoMaximum)).

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- not_min_max([3, 2], NotMinMax).  

NotMinMax = -1

yes
| ?- not_min_max([3, 2, 1, 4], NotMinMax). 

NotMinMax = [3,2]

yes
| ?- not_min_max([1, 3, 2], NotMinMax).

NotMinMax = [2]

yes

Notes

This is about as straightforward a solution as you can get in Prolog. All the details can be handled by built in predicates. That is, finding the minimum and maximum values, removing those values from consideration are all done for us. The only complication comes fromt he stipulation that we should return -1 instead of the empty list. This isn't a very Prolog thing to do! These problems are not written with Prolog in mind, however, and we make it work easily enough anyway.

Part 2

You are given a list of passenger details in the form “9999999999A1122”, where 9 denotes the phone number, A the sex, 1 the age and 2 the seat number. Write a script to return the count of all senior citizens (age >= 60).

Solution

passenger_senior(Passenger, Senior):-
    length(AgeSeat, 4),
    length(Age, 2),
    atom_chars(Passenger, PassengerChars),
    suffix(AgeSeat, PassengerChars),
    prefix(Age, AgeSeat),
    number_chars(A, Age),
    ((A >= 60, Senior = 1); Senior = 0).

count_senior_citizens(Passengers, CountSeniorCitizens):-
    maplist(passenger_senior, Passengers, SeniorCitizens), !,
    sum_list(SeniorCitizens, CountSeniorCitizens).

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- count_senior_citizens(['7868190130M7522', '5303914400F9211', '9273338290F4010'], Count).

Count = 2

(1 ms) yes
| ?- count_senior_citizens(['1313579440F2036', '2921522980M5644'], Count).   

Count = 0

yes
| ?-

Notes

Since the passenger details are given in strings with fixed width fields we can chop up and find what we need using lists. Since the information we seek (the age) is at the end of the passenger details we can work from the suffix. First we get the details as characters, then we get the final four characters. Of these final four the first two are the age.

This is all done by way of maplist/3. Only those passengers that meet the age criteria are given a value of one, the rest zero. The final count is taken via sum_list/2.

References

Challenge 231

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of distinct integers. Write a script to find all elements that is neither minimum nor maximum. Return -1 if you can’t.

Solution

use v5.38;
sub not_min_max{
    my($minimum, $maximum);
    do{
        $minimum = $_ if !$minimum || $_ < $minimum;
        $maximum = $_ if !$maximum || $_ > $maximum;
    } for @_;
    my @r = grep { $_ ^ $minimum && $_ ^ $maximum } @_;
    return @r ^ 0 ? @r : -1;
}

MAIN:{
    say join q/, /, not_min_max 3, 2, 1, 4;
    say join q/, /, not_min_max 3, 1;
    say join q/, /, not_min_max 2, 1, 3;
}

Sample Run

$ perl perl/ch-1.pl 
3, 2
-1
2

Notes

Once we find the maximum and minimum values, we need to remove them. Just to be different I used the XOR ^ operator instead of !=. The effect is the same, a false (zero) value is returned if the values are identical, true (one) otherwise.

Part 2

You are given a list of passenger details in the form “9999999999A1122”, where 9 denotes the phone number, A the sex, 1 the age and 2 the seat number. Write a script to return the count of all senior citizens (age >= 60).

Solution

use v5.38;
sub count_senior_citizens{
    my $count = 0;
    do{
        my @a = unpack q/A10A1A2A2/, $_; 
        $count++ if $a[2] >= 60;
    } for @_;
    return $count;
}

MAIN:{
    say count_senior_citizens qw/7868190130M7522 5303914400F9211 9273338290F4010/;
    say count_senior_citizens qw/1313579440F2036 2921522980M5644/;
}

Sample Run

$ perl perl/ch-2.pl 
2
0

Notes

It isn't all that often you find a nice clean use of unpack! This seems to be a very nice opportunity: each passenger string has fixed field lengths.

The passenger strings themselves are just Perl scalar values. They are not, say, specially constructed strings via pack. To unpack an ordinary scalar we can just use As in the template string.

References

pack/unpack Templates

Challenge 231

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of positive integers. Write a script to separate the given array into single digits.

Solution

clone(X, [X]).

separate(Number, Digits):-
    number_chars(Number, Chars),
    maplist(clone, Chars, DigitChars),
    maplist(number_chars, Digits, DigitChars).

separate_digits(Numbers, Digits):-
    maplist(separate, Numbers, D),
    flatten(D, Digits).

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- separate_digits([1, 34, 5, 6], Digits).

Digits = [1,3,4,5,6] ? 

yes

Notes

For a long time I really never embraced the full power of maplist. At present I can't seem to get enough! In this solution to TWC230.1 we use maplist to first create a singleton list for each digit character in each of the given numbers, we then use maplist to convert these singleton lists to single digit numbers as required.

Part 2

You are given an array of words made up of alphabetic characters and a prefix. Write a script to return the count of words that starts with the given prefix.

Solution

prefix_match(Prefix, Word, Match):-
    atom_chars(Prefix, PrefixChars),
    atom_chars(Word, WordChars),
    ((prefix(PrefixChars, WordChars), Match = 1);
     (\+ prefix(PrefixChars, WordChars), Match = 0)).

count_words(Prefix, Words, Count):-
    maplist(prefix_match(Prefix), Words, Matches),
    sum_list(Matches, Count).

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- count_words(at, [pay, attention, practice, attend], Count).

Count = 2 ? 

yes
| ?- count_words(ja, [janet, julia, java, javascript], Count).  

Count = 3 ? 

(1 ms) yes
| ?- 

Notes

Another nice use of maplist, but a bit less gratuitous. In this solution to TWC230.2 we use maplist to generate a list of 0s or 1s, depending on whether a given word starts with the given prefix. The count of matching words is then the sum_list/2 of those results.

References

Challenge 230

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of positive integers. Write a script to separate the given array into single digits.

Solution

use v5.38;
sub separate_digits{
    return separater([], @_); 
}

sub separater{
    my $seperated = shift;
    return @{$seperated} if @_ == 0;
    my @digits = @_;
    push @{$seperated}, split //, shift @digits;
    separater($seperated, @digits);
}

MAIN:{
    say join q/,/, separate_digits 1, 34, 5, 6;
}

Sample Run

$ perl perl/ch-1.pl 
1,3,4,5,6

Notes

It has been a while since I wrote recursive Perl code, this week's TWC offered two nice chances to do so. The first call to separate_digits invokes the call to the recursive subroutine separater, adding an array reference for the convenience of accumulating the individual digits at each recursive step.

Within separater each number in the array is taken one at a time and expanded to its individual digits. The digits are pushed into the accumulator. When we run of digits we return the complete list of digits.

Part 2

You are given an array of words made up of alphabetic characters and a prefix. Write a script to return the count of words that starts with the given prefix.

Solution

use v5.38;
sub count_words{
    return counter(0, @_); 
}

sub counter{
    my $count = shift;
    my $prefix = shift;
    return $count if @_ == 0;
    my $word = shift;
    $count++ if $word =~ m/^$prefix/;
    counter($count, $prefix, @_);
}

MAIN:{
    say count_words qw/at pay attention practice attend/;
    say count_words qw/ja janet julia java javascript/;
}

Sample Run

$ perl perl/ch-2.pl 
2
3

Notes

The exact same approach used for Part 1 is used here in the second part. Instead of accumulating am array of digits instead we increment the counter of words which start with the prefix characters.

References

Challenge 230

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a string and an array of indices of same length as string. Write a script to return the string after re-arranging the indices in the correct order.

Solution

use v5.38;
sub shuffle_string{
    my($s, $indices) = @_;
    my @s = split(//, $s);
    my @t;
    do { $t[$_] = shift @s } for @{$indices};
    return join(q//, @t);
}

MAIN:{
    say shuffle_string(q/lacelengh/, [3, 2, 0, 5, 4, 8, 6, 7, 1]);
    say shuffle_string(q/rulepark/, [4, 7, 3, 1, 0, 5, 2, 6]);
}

Sample Run

$ perl perl/ch-1.pl 
challenge
perlraku

Notes

I had to think of this one a bit! What we need to do is take each letter, from left to right, and assign it a new position. It's not often you see a shift within another loop but here that is the key to getting everything working.

Part 2

You are given an array of non-negative integers, @ints. Write a script to return the minimum number of operations to make every element equal zero.

Solution

use v5.38;
sub zero_array{
    my $operations = 0;
    do{
        return $operations if 0 == unpack(q/%32I*/, pack(q/I*/, @_));
        my $minimum = (sort { $a <=> $b } grep { $_ > 0 } @_)[0];
        @_ = map { $_ > 0 ? $_ - $minimum : 0 } @_; 
        $operations++;
    } for @_;
}

MAIN:{
    say zero_array 1, 5, 0, 3, 5;
    say zero_array 0;
    say zero_array 2, 1, 4, 0, 3
}

Sample Run

$ perl perl/ch-2.pl 
3
0
4

Notes

Usually I assign function arguments new names, even if I am just passing in a single array of values like in this example. I decided this time to not do it, I don't think readability is sacrificed. Provided the reader actually knows what @_ is I think for a short function such as this it's fine. In fact, I think an argument could be made that readability is actually enhanced since lines such as the one with both a sort and a grep are kept to a shorter length.

References

Challenge 226

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a string and an array of indices of same length as string. Write a script to return the string after re-arranging the indices in the correct order.

Solution

letter_shuffle(Shuffled, Letter, Index):-
    nth(Index, Shuffled, Letter).

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- length(L, 9), maplist(letter_shuffle(L), "lacelengh", [4, 3, 1, 6, 5, 9, 7, 8, 2]), atom_codes(A, L).

A = challenge
L = [99,104,97,108,108,101,110,103,101]

yes

Notes

Many Prologs, including GNU Prolog, treat double quoted strings as lists of the character codes representing each letter. So here maplist/3 is presented such a list as well as the given list of indices. We give a letter_shuffle/3 an empty list of the right length and all that is left is for nth/3 to assign the letters as needed.

Part 2

You are given an array of non-negative integers, @ints. Write a script to return the minimum number of operations to make every element equal zero.

Solution

subtract_minimum(Minimum, X, Y):-
    Y is X - Minimum.

zero_array(Numbers, Operations):-
    delete(Numbers, 0, NumbersNoZero),
    zero_array(NumbersNoZero, 0, Operations).
zero_array([], Operations, Operations).    
zero_array(Numbers, OperationsCounter, Operations):-
    delete(Numbers, 0, NumbersNoZero),
    min_list(NumbersNoZero, Minimum),
    maplist(subtract_minimum(Minimum), NumbersNoZero, NumbersSubtracted),
    succ(OperationsCounter, OperationsCounterNext), 
    delete(NumbersSubtracted, 0, NumbersSubtractedNoZero),
    zero_array(NumbersSubtractedNoZero, OperationsCounterNext, Operations).

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- zero_array([1, 5, 0, 3, 5], Operations).

Operations = 3 ? 

yes
| ?- zero_array([0], Operations).

Operations = 0 ? 

yes
| ?- zero_array([2, 1, 4, 0, 3], Operations).

Operations = 4 ? 

yes
| ?- 

Notes

A convenient issue with this problem is that once a list entry is zero we can ignore it. Since we can ignore it we can delete/3 it and thereby reduce the list eventually to the empty list, the base of our recursion. Each time we recurse we find the minimum element, subtract it from all others, and increment the number of operations.

References

Challenge 226

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a list of sentences. Write a script to find out the maximum number of words that appear in a single sentence.

Solution

use v5.38;
sub max_sentence_length{
    my(@sentences) = @_;
    my $max_words = -1;
    do{
        my @word_matches = $_ =~ m/(\w+)/g; 
        $max_words = @word_matches if @word_matches > $max_words;
    } for @sentences;
    return $max_words;
}

MAIN:{
    my @list;
    @list = ("Perl and Raku belong to the same family.", "I love Perl.", 
"The Perl and Raku Conference.");
    say  max_sentence_length(@list);
    @list = ("The Weekly Challenge.", "Python is the most popular guest language.",
"Team PWC has over 300 members.");
    say  max_sentence_length(@list);
}

Sample Run

$ perl perl/ch-1.pl 
8
7

Notes

This is the perfect job for a regular expression! In fact \w is a special character sequence which matches word characters, so they heart of the solution is to apply it to the given sentences and count the matches.

The expression my @word_matches = $_ =~ m/(\w+)/g may look a little weird at first. What is happening here is that we are collecting all groups of matchs (enclosed in parentheses in the regex) into a single array. In this way, we immediately know the number of words in each sentence, it is just the size of the array.

Part 2

You are given an array of integers. Write a script to return left right sum difference array.

Solution

use v5.38;
sub left_right_sum{
    return unpack("%32I*", pack("I*", @_));
}

sub left_right_differences{
    my(@left_sum, @right_sum);
    for(my $i = 0; $i < @_; $i++){
        push @left_sum, left_right_sum(@_[0 .. $i - 1]);
        push @right_sum, left_right_sum(@_[$i + 1 .. @_ - 1]);
    }    
    return map { abs($left_sum[$_] - $right_sum[$_]) } 0 .. @_ - 1;
}

MAIN:{
    say join(q/, /, left_right_differences 10, 4, 8, 3);
    say join(q/, /, left_right_differences 1);
    say join(q/, /, left_right_differences 1, 2, 3, 4, 5);
}

Sample Run

$ perl perl/ch-2.pl 
15, 1, 11, 22
0
14, 11, 6, 1, 10

Notes

The problem statement may be a little confusing at first. What we are trying to do here is to get two lists the prefix sums and suffix sums, also called the left and right sums. We then pairwise take the absolute values of each element in these lists to get the final result. Iterating over the list the prefix sums are the partial sums of the list elements to the left of the current element. The suffix sums are the partial sums of the list elements to the right of the current element.

With that understanding in hand the solution becomes much more clear! We iterate over the list and then using slices get the prefix and suffix arrays for each element. Using my favorite way to sum a list of numbers, left_right_sum() does the job with pack/unpack. Finally, a map computes the set of differences.

References

Challenge 225

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a list of sentences. Write a script to find out the maximum number of words that appear in a single sentence.

Solution

check_and_read(32, [], _):-
    !.
check_and_read(46, [], _):-
    !. 
check_and_read(-1, [], _):-
    !.
check_and_read(Char, [Char|Chars], Stream):-
    get_code(Stream, NextChar),
    check_and_read(NextChar, Chars, Stream).

read_data(Stream, []):-
    at_end_of_stream(Stream).
read_data(Stream, [X|L]):-
    \+ at_end_of_stream(Stream),
    get_code(Stream, Char),
    check_and_read(Char, Chars, Stream),
    atom_codes(X, Chars),
    read_data(Stream, L).

sentence_atoms(Sentence, Atoms):-
    open_input_codes_stream(Sentence, Stream),
    read_data(Stream, Atoms).

max_sentence_length(Sentences, MaxLength):-
    maplist(sentence_atoms, Sentences, SentenceAtoms),
    maplist(length, SentenceAtoms, Lengths),
    max_list(Lengths, MaxLength).

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- max_sentence_length(["Perl and Raku belong to the same family.", "I love Perl.", "The Perl and Raku Conference."], MaxLength).            

MaxLength = 8 ? 

yes
| ?- max_sentence_length(["The Weekly Challenge.", "Python is the most popular guest language.", "Team PWC has over 300 members."], MaxLength).

MaxLength = 7 ? 

yes
| ?- 

Notes

Since these are programming challenges which are designed with Perl in mind the inputs sometimes require a little manipulation to make them more Prolog friendly. In this case the sentence strings need to be turned into lists of atoms. This is done here by use of Stream processing!

I don't think I've had much occasion to use open_input_codes_stream/2 before. What this does is take the double quoted string, which is seen by Prolog as a list of character codes, and open this as a Stream. We can then process this in the same way as we'd process any other input stream, more typically a file. In fact, much of the code for processing this Stream is re-used from other such code.

The solution, then, is that max_sentence_length/2 will take a list of sentences, call senetence_atoms/2 via a maplist/3 to get a list of list of atoms, then again with a maplist/3 get the lengths of the atom lists, and then finally get the maximum sentence length (the result) from max_list/2.

Part 2

You are given an array of integers. Write a script to return left right sum difference array.

Solution

difference(X, Y, Z):-
    Z is abs(X - Y).

differences(_, 0, LeftAccum, RightAccum, LeftRightDifferences):-
    maplist(difference, LeftAccum, RightAccum, LeftRightDifferences).
differences(Numbers, Index, LeftAccum, RightAccum, LeftRightDifferences):-
    length(Numbers, L),
    Left is Index - 1,
    Right is L - Index,
    length(Prefix, Left),
    length(Suffix, Right),
    prefix(Prefix, Numbers),
    suffix(Suffix, Numbers),
    sum_list(Prefix, LeftSum),
    sum_list(Suffix, RightSum),
    succ(IndexNext, Index),
    differences(Numbers, IndexNext, [LeftSum|LeftAccum], [RightSum|RightAccum], LeftRightDifferences).

left_right_differences(Numbers, LeftRightDifferences):-
    length(Numbers, L),
    differences(Numbers, L, [], [], LeftRightDifferences).

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- left_right_differences([10, 4, 8, 3], LeftRightDifferences).

LeftRightDifferences = [15,1,11,22] ? 

yes
| ?- left_right_differences([1], LeftRightDifferences). 

LeftRightDifferences = [0] ? 

yes
| ?- left_right_differences([1, 2, 3, 4, 5], LeftRightDifferences).

LeftRightDifferences = [14,11,6,1,10] ? 

(1 ms) yes
| ?- 

Notes

The problem statement may be a little confusing at first. What we are trying to do here is to get two lists the prefix sums and suffix sums, also called the left and right sums. We then pairwise take the absolute values of each element in these lists to get the final result. Recursively iterating over the list the prefix sums are the partial sums of the list elements to the left of the current element. The suffix sums are the partial sums of the list elements to the right of the current element.

Once the problem is understood the components of the solution start to come together:

1. Iterate over the original list and build up the partial sums. prefix/2, suffix/2, and sum_list/2 are very helpful here!
2. When we are done building the lists of partial sums take the pairwise differences. This could also be done iteratively, but more elegantly we can make use of maplist/4.
3. Our use of maplist/4 uses the small utility predicate difference/3.

References

Challenge 225

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of integers. Write a script to print 1 if there are THREE consecutive odds in the given array otherwise print 0.

Solution

use v5.36;
use boolean;

sub three_consecutive_odds{
    my @numbers = @_;
    my $consecutive_odds = 0;
    {
        my $x = pop @numbers;
        $consecutive_odds++   if 1 == ($x & 1);
        $consecutive_odds = 0 if 0 == ($x & 1);
        return true if 3 == $consecutive_odds;
        redo if @numbers;
    }
    return false;
}

MAIN:{
    say three_consecutive_odds(1, 5, 3, 6);
    say three_consecutive_odds(2, 6, 3, 5);
    say three_consecutive_odds(1, 2, 3, 4);
    say three_consecutive_odds(2, 3, 5, 7);
}

Sample Run

$ perl perl/ch-1.pl 
1
0
0
1

Notes

Part 2

Given a profile as a list of altitudes, return the leftmost widest valley. A valley is defined as a subarray of the profile consisting of two parts: the first part is non-increasing and the second part is non-decreasing. Either part can be empty.

Solution

use v5.36;
use boolean;
use FSA::Rules;

sub widest_valley_rules{
    my @altitudes = @_;
    my @downslope;
    my @upslope;
    my $fsa = FSA::Rules->new(
        move => {
            do => sub{  my $state = shift;
                        $state->machine->{altitude}  = [] if(!$state->machine->{altitude});
                        $state->machine->{plateau}   = [] if(!$state->machine->{plateau});
                        $state->machine->{downslope} = [] if(!$state->machine->{downslope});
                        $state->machine->{upslope}   = [] if(!$state->machine->{upslope});
                        my $previous_altitudes = $state->machine->{altitude};
                        my $current_altitude = shift @altitudes;
                        push @{$previous_altitudes}, $current_altitude
            },
            rules => [ done      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          !defined($previous_altitudes->[@{$previous_altitudes} - 1]) 
                       },
                       move      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          @{$previous_altitudes} ==  1; 
                       },
                       plateau   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if(@{$previous_altitudes} == 2){
                                              if($previous_altitudes->[@{$previous_altitudes} - 1] == $previous_altitudes->[@{$previous_altitudes} - 2]){
                                                  push @{$state->machine->{plateau}}, $previous_altitudes->[@{$previous_altitudes} - 2], $previous_altitudes->[@{$previous_altitudes} - 1];
                                              }
                                          }
                       },
                       plateau   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if(@{$previous_altitudes} > 2){
                                              if($previous_altitudes->[@{$previous_altitudes} - 1] == $previous_altitudes->[@{$previous_altitudes} - 2]){
                                                  push @{$state->machine->{plateau}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                              }
                                          }
                       },
                       downslope => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if(@{$previous_altitudes} == 2){
                                              if($previous_altitudes->[@{$previous_altitudes} - 1] < $previous_altitudes->[@{$previous_altitudes} - 2]){
                                                  push @{$state->machine->{downslope}}, $previous_altitudes->[@{$previous_altitudes} - 2], $previous_altitudes->[@{$previous_altitudes} - 1];
                                              }
                                          }
                       },
                       downslope => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if(@{$previous_altitudes} > 2){
                                              if($previous_altitudes->[@{$previous_altitudes} - 1] < $previous_altitudes->[@{$previous_altitudes} - 2]){
                                                  push @{$state->machine->{downslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                              }else{false}
                                          } 
                       },
                       upslope => sub{  my $state = shift; 
                                        my $previous_altitudes = $state->machine->{altitude}; 
                                        if(@{$previous_altitudes} == 2){
                                           if($previous_altitudes->[@{$previous_altitudes} - 1] > $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{upslope}}, $previous_altitudes->[@{$previous_altitudes} - 2], $previous_altitudes->[@{$previous_altitudes} - 1];
                                           }
                                        } 
                       },
                       upslope => sub{  my $state = shift; 
                                        my $previous_altitudes = $state->machine->{altitude}; 
                                        if(@{$previous_altitudes} > 2){
                                           if($previous_altitudes->[@{$previous_altitudes} - 1] > $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{upslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                           }
                                        } 
                       },
            ],
        },
        plateau => {             
            do => sub{  my $state = shift;
                        my $previous_altitudes = $state->machine->{altitude}; 
                        my $current_altitude = shift @altitudes; 
                        push @{$previous_altitudes}, $current_altitude;
            },
            rules => [ done      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          !defined($previous_altitudes->[@{$previous_altitudes} - 1]) 
                       },  
                       plateau   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] == $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{plateau}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                          }
                       },       
                       downslope => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] < $previous_altitudes->[@{$previous_altitudes} - 2]){
                                              push @{$state->machine->{downslope}}, @{$state->machine->{plateau}};
                                              push @{$state->machine->{downslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                              $state->machine->{plateau} = [];
                                          }
                       },
                       upslope   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] > $previous_altitudes->[@{$previous_altitudes} - 2]){
                                              push @{$state->machine->{upslope}}, @{$state->machine->{plateau}};
                                              push @{$state->machine->{upslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                              $state->machine->{plateau} = [];
                                          }
                       }        
            ], 
        },
        downslope => {
            do => sub{  my $state = shift;
                        my $previous_altitudes = $state->machine->{altitude}; 
                        my $current_altitude = shift @altitudes;
                        push @{$previous_altitudes}, $current_altitude;
            },
            rules => [ done      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          !defined($previous_altitudes->[@{$previous_altitudes} - 1]) 
                       },   
                       plateau   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] == $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{plateau}}, $previous_altitudes->[@{$previous_altitudes} - 2], $previous_altitudes->[@{$previous_altitudes} - 1];
                                               #pop @{$state->machine->{downslope}};true;
                                          }
                       },      
                       downslope => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] < $previous_altitudes->[@{$previous_altitudes} - 2]){
                                              push @{$state->machine->{downslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                          } 
                                    },
                       upslope   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] > $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               $state->machine->{upslope} = [];
                                               push @{$state->machine->{upslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                          } 
                                    },      
            ], 
        },
        upslope => {             
            do => sub{  my $state = shift;
                        my $previous_altitudes = $state->machine->{altitude}; 
                        my $current_altitude = shift @altitudes;
                        push @{$previous_altitudes}, $current_altitude; 
            },
            rules => [ done      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          !defined($previous_altitudes->[@{$previous_altitudes} - 1]) 
                       },   
                       done      => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          $previous_altitudes->[@{$previous_altitudes} - 1] < $previous_altitudes->[@{$previous_altitudes} - 2];
                       }, 
                       plateau   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] == $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{plateau}}, $previous_altitudes->[@{$previous_altitudes} - 2], $previous_altitudes->[@{$previous_altitudes} - 1];
                                          }
                       },   
                       upslope   => sub{  my $state = shift; 
                                          my $previous_altitudes = $state->machine->{altitude}; 
                                          if($previous_altitudes->[@{$previous_altitudes} - 1] > $previous_altitudes->[@{$previous_altitudes} - 2]){
                                               push @{$state->machine->{upslope}}, $previous_altitudes->[@{$previous_altitudes} - 1];
                                          }
                       }        
            ], 
        },
        done => { 
            do => sub { my $state = shift; 
                        say q/Valley: / . join(q/, /,  @{$state->machine->{downslope}}, @{$state->machine->{upslope}});
                  } 
        },
    );
    return $fsa;
}

sub widest_valley{
    my $rules = widest_valley_rules(@_);
    $rules->start;
    $rules->switch until $rules->at(q/done/);
    my $graph_viz = $rules->graph();
}

MAIN:{
    widest_valley 1, 5, 5, 2, 8;
    widest_valley 2, 6, 8, 5;
    widest_valley 2, 1, 2, 1, 3;
}

Sample Run

$ perl perl/ch-2.pl 
Valley: 5, 5, 2, 8
Valley: 2, 6, 8
Valley: 2, 1, 2

Notes

References

Challenge 202

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of unique numbers. Write a script to find out all missing numbers in the range 0..$n where $n is the array size.

Solution

missing_number(Numbers, Missing):-
    length(Numbers, NumbersLength),
    between(0, NumbersLength, Missing),
    \+ member(Missing, Numbers). 

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- missing_number([0, 1, 3], Missing).

Missing = 2 ? 

(1 ms) yes
| ?- missing_number([0, 1], Missing).   

Missing = 2

yes
| ?- 

Notes

missing_number/2 will only find one missing number at a time. In the examples that come with the original problem statement there is only ever one missing number. If multiple missing numbers are required backtracking with findall/3 is all you need!

Part 2

You are given an integer, $n > 0. Write a script to determine the number of ways of putting $n pennies in a row of piles of ascending heights from left to right.

Solution

sum(Coins):-
    sum([], Coins, 0).

sum(Coins, Coins, 5). 

sum(Partial, Coins, Sum):-   
    Sum < 5, 
    between(1, 5, X),
    S is Sum + X,
    sum([X | Partial], Coins, S).  

main:-
    findall(Coins, sum(Coins), C),
    maplist(msort, C, CS),
    sort(CS, CoinsSorted),
    write(CoinsSorted), nl,
    halt.  

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- main.
[[1,1,1,1,1],[1,1,1,2],[1,1,3],[1,2,2],[1,4],[2,3],[5]]

Notes

The approach here is the same that I used for the Coins Sum problem from TWC 075. The same as for the Perl solution to the same problem.

References

Challenge 201

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given an array of unique numbers. Write a script to find out all missing numbers in the range 0..$n where $n is the array size.

Solution

use v5.36;
use boolean;
sub missing_numbers{
    my @numbers = @_;
    my %h;
    do { $h{$_} = undef } for @numbers;
    my @missing = grep { !exists($h{$_}) } 0 .. @numbers;
    return @missing;
}

MAIN:{
    say q/(/ . join(q/, /, missing_numbers(0, 1, 3)) . q/)/;
    say q/(/ . join(q/, /, missing_numbers(0, 1)) . q/)/;
    say q/(/ . join(q/, /, missing_numbers(0, 1, 2, 2)) . q/)/;
}

Sample Run

$ perl perl/ch-1.pl 
(2)
(2)
(3, 4)

Notes

This problem was a nice refresh on exists, which is often confused with defined. Here we want to see if the hash key exists at all and so the use is appropriate. If we had wanted to see if the value keyed was defined, well, that is the use for defined!

Part 2

You are given an integer, $n > 0. Write a script to determine the number of ways of putting $n pennies in a row of piles of ascending heights from left to right.

Solution

use v5.36;
use AI::Prolog;
use Hash::MultiKey;

MAIN:{
    my $S = $ARGV[0];
    my $C = "[" . $ARGV[1] . "]";

    my $prolog = do{
        local $/;
        <DATA>;
    }; 
    $prolog =~ s/_COINS_/$C/g;
    $prolog =~ s/_SUM_/$S/g;
    $prolog = AI::Prolog->new($prolog); 
    $prolog->query("sum(Coins).");
    my %h;
    tie %h, "Hash::MultiKey";
    while(my $result = $prolog->results){
        my @s = sort @{$result->[1]};
        $h{\@s} = undef;
    }
    for my $k ( sort { @{$b} <=> @{$a} } keys %h){
        print "(" . join(",", @{$k}) . ")";
        print "\n";
    }
}

__DATA__
member(X,[X|_]).
member(X,[_|T]) :- member(X,T).

coins(_COINS_).

sum(Coins):-
    sum([], Coins, 0).

sum(Coins, Coins, _SUM_). 

sum(Partial, Coins, Sum):-   
    Sum < _SUM_, 
    coins(L),
    member(X,L),
    S is Sum + X,
    sum([X | Partial], Coins, S). 

Sample Run

$ perl perl/ch-2.pl 5 1,2,3,4,5
(1,1,1,1,1)
(1,1,1,2)
(1,2,2)
(1,1,3)
(1,4)
(2,3)
(5)

Notes

The approach here is the same that I used for the Coins Sum problem from TWC 075. The only change is the added sort by the length of the "piles".

References

Challenge 201

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a list of integers, @list. Write a script to find the total count of Good airs.

Solution

good_pair(Numbers, Pair):-
    length(Numbers, L),
    fd_domain(I, 1, L),
    fd_domain(J, 1, L),
    I #<# J,
    fd_labeling([I, J]), 
    fd_element(I, Numbers, Ith),  
    fd_element(J, Numbers, Jth), 
    Ith #= Jth,
    Pair = [I, J].   

Sample Run

$ gprolog --consult-file prolog/ch-1.p
| ?- good_pair([1, 2, 3, 1, 1, 3], Pair).

Pair = [1,4] ? a

Pair = [1,5]

Pair = [3,6]

Pair = [4,5]

no
| ?- good_pair([1, 2, 3], Pair).         

no
| ?- good_pair([1, 1, 1, 1], Pair).

Pair = [1,2] ? a

Pair = [1,3]

Pair = [1,4]

Pair = [2,3]

Pair = [2,4]

Pair = [3,4]

yes
| ?- 

Notes

I take a clpfd approach to this problem and the next. This allows a pretty concise solution. Here we get the length of the list of numbers, constrain the indices for the pair and then specify the additional conditions of a Good Pair.

Part 2

You are given an array of integers, @array and three integers $x,$y,$z. Write a script to find out total Good Triplets in the given array.

Solution

good_triplet(Numbers, X, Y, Z, Triplet):-
    length(Numbers, I),
    fd_domain(S, 1, I),
    fd_domain(T, 1, I),
    fd_domain(U, 1, I),
    S #<# T, T #<# U,   
    fd_labeling([S, T, U]),   
    fd_element(S, Numbers, Sth),  
    fd_element(T, Numbers, Tth),  
    fd_element(U, Numbers, Uth), 
    Ast is abs(Sth - Tth), Ast #=<# X,     
    Atu is abs(Tth - Uth), Atu #=<# Y,     
    Asu is abs(Sth - Uth), Asu #=<# Z, 
    Triplet = [Sth, Tth, Uth].   

Sample Run

$ gprolog --consult-file prolog/ch-2.p
| ?- good_triplet([3, 0, 1, 1, 9, 7], 7, 2, 3, Triplet).

Triplet = [3,0,1] ? a

Triplet = [3,0,1]

Triplet = [3,1,1]

Triplet = [0,1,1]

no
| ?- good_triplet([1, 1, 2, 2, 3], 0, 0, 1, Triplet).   

no
| ?-

Notes

Again for part 2 a clpfd solution ends up being fairly concise. In fact, the approach here is virtually identical to part 1. The differences are only that we are looking for a triple, not a pair, and slightly different criteria.

References

Challenge 199

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a list of integers, @list. Write a script to find the total count of Good airs.

Solution

use v5.36;
sub good_pairs{
    my(@numbers) = @_;
    my @pairs;  
    do{ 
        my $i = $_;
        do{
            my $j = $_;
            push @pairs, [$i, $j] if $numbers[$i] == $numbers[$j] && $i < $j;  
        } for 0 .. @numbers - 1;
    } for 0 .. @numbers - 1;
    return 0 + @pairs;  
}

MAIN:{
    say good_pairs 1, 2, 3, 1, 1, 3;
    say good_pairs 1, 2, 3;
    say good_pairs 1, 1, 1, 1;
}

Sample Run

$ perl perl/ch-1.pl 
4
0
6

Notes

First off, a pair (i, j) is called good if list[i] == list[j] and i < j. Secondly, I have never written a nested loop with this mix of do blocks and postfix for, and I am greatly entertained by it! Perl fans will know that it really isn't all that different from the more standard looking do/while construct. A do block is not really a loop, although it can be repeated, and so you cannot use last, redo, or next within the block. But this is exactly the same case as within a map, which is what we are trying to replicate here, a map in void context without actually using map.

Imagine a nested map, that is basically the same thing as this, but with the more clear focus on side effects versus a return value.

Part 2

You are given an array of integers, @array and three integers $x,$y,$z. Write a script to find out total Good Triplets in the given array.

Solution

use v5.36;
use Math::Combinatorics;
sub good_triplets{
    my($numbers, $x, $y, $z) = @_;
    my $combinations = Math::Combinatorics->new(count => 3, data => [0 .. @{$numbers} - 1]);
    my @combination = $combinations->next_combination;  
    my @good_triplets;
    {
        my($s, $t, $u) = @combination;
        unless($s >= $t || $t >= $u || $s >= $u){
            push @good_triplets, [@{$numbers}[$s, $t, $u]] if(abs($numbers->[$s] - $numbers->[$t]) <= $x && 
                                                              abs($numbers->[$t] - $numbers->[$u]) <= $y &&  
                                                              abs($numbers->[$s] - $numbers->[$u]) <= $z);  

    }
        @combination = $combinations->next_combination;  
        redo if @combination;
    }
    return 0 + @good_triplets;
}

MAIN:{
    say good_triplets([3, 0, 1, 1, 9, 7], 7, 2, 3);
    say good_triplets([1, 1, 2, 2, 3], 0, 0, 1);
}

Sample Run

$ perl perl/ch-2.pl
4
0

Notes

The approach here is the same that I used for the Magical Triples problem from TWC 187. The module Math::Combinatorics is used to generate all possible triples of indices. These are then filtered according to the criteria for good triplets.

References

Challenge 199

The examples used here are from the weekly challenge problem statement and demonstrate the working solution.

Part 1

You are given a list of integers, @list. Write a script to find the total pairs in the sorted list where 2 consecutive elements has the max gap. If the list contains less then 2 elements then return 0.

Solution

use v5.36;
sub largest_gap{
    my(@numbers) = @_;
    my $gap = -1;
    map{ $gap = $numbers[$_] - $numbers[$_ - 1] if $numbers[$_] - $numbers[$_ - 1] > $gap } 1 .. @numbers - 1;  
    return $gap;
}

sub gap_pairs{
    my(@numbers) = @_;
    return 0 if @numbers < 2; 
    my $gap = largest_gap(@numbers);
    my $gap_count;
    map { $gap_count++ if $numbers[$_] - $numbers[$_ - 1] == $gap } 1 .. @numbers - 1;  
    return $gap_count;

}

MAIN:{
    say gap_pairs(3);    
    say gap_pairs(2, 5, 8, 1);    
}

Sample Run

$ perl perl/ch-1.pl 
0
2

Notes

Probably these two subroutines could be combined into one without too much trouble, but it still seems cleaner to me this way.

1. Do an initial pass over the list to determine the largest gap.

2. Perform a second pass over the list and count up all pairs which have the maximum gap.

An interesting issue came up. I've been trying to avoid the use of a map in a void context. This is just due to the general principal to use map as a function and use its return value rather than rely on side effects.

As part of this reformative effort I have been doing more with for in a postfix position. I discovered this when working this problem:

{say $_ if $_ % 2 == 0} for 0 .. 9 will not work. Perl gets confused by the postfix if within the block, apparently.

But there is a work around! Add do and all is well.

do {say $_ if $_ % 2 == 0} for 0 .. 9

Of course the equivalent map works just fine as you'd expect map {say $_ if $_ % 2 == 0} 0 .. 9)

E. Choroba pointed out this is due to postfix for being a statement modifier which doesn't know what to do with blocks. But why does do fix this? I am still unclear on why that is. Even with the do it's still a block! Apparently perl will view it as a statement, for the purposes of the postfix for?

UPDATE: Turns out that the do {} construct qualifies as a Simple Statement. From the perldoc: Note that there are operators like eval {}, sub {}, and do {} that look like compound statements, but aren't--they're just TERMs in an expression--and thus need an explicit termination when used as the last item in a statement.

Part 2

You are given an integer $n > 0. Write a script to print the count of primes less than $n.

Solution

use v5.36;
use Math::Primality q/is_prime/;

sub prime_count{
    return 0 + grep { is_prime $_ } 2 .. $_[0] - 1;  
}

MAIN:{
    say prime_count(10);  
    say prime_count(15);  
    say prime_count(1);  
    say prime_count(25);  
}

Sample Run

$ perl perl/ch-2.pl
4
6
0
9

Notes

The Math::Primality module makes this quite easy! In fact, I am not sure there is that much to elaborate on. Check primality using is_prime() and we're done!

References

Challenge 198